题目内容
3.(1)解方程:x2+4x-5=0(配方法)(2)已知:关于x的方程2x2+kx-1=0.
①求证:方程有两个不相等的实数根;②若方程的一个根是-1,求另一个根及k值.
分析 (1)把常数项-5移项后,应该在左右两边同时加上一次项系数4的一半的平方.
(2)①由△=b2-4ac=k2+8>0,即可判定方程有两个不相等的实数根;
②首先将x=-1代入原方程,求得k的值,然后解此方程即可求得另一个根.
解答 解:由原方程移项,得
x2+4x=5,
方程两边同时加上一次项系数一半的平方,得到x2+4x+4=5+4,
配方得(x+2)2=9.
开方,得
x+2=±3,
解得x1=1,x2=-5.
(2)①∵△=k2+8>0,
∴方程有两个不相等的实数根;
②当x=-1时,2×(-1)2-k-1=0,
解得:k=1,
则原方程为:2x2+x-2=0,
即(2x-1)(x+1)=0,
解得:x1=0.5,x2=-1,
所以另一个根为0.5.
点评 此题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.也考查了用配方法解一元二次方程.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
11.下面说法中正确的是( )
| A. | 真分数小于1,假分数大于1 | B. | 小于1的真分数有4个 | ||
| C. | 最简分数的分子和分母没有公约数 | D. | 假分数的倒数不一定是真分数 |
5.一件衣服提高价格25%后发现销路不是很好,欲恢复原价,则应降价( )
| A. | 40% | B. | 20% | C. | 25% | D. | 15% |
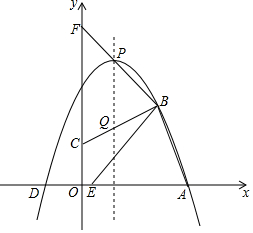 如图,二次函数y=ax2+bxc的图象经过A(4,0),D(-1,0)和B(3,3)三,.顶点为点P.作BC⊥BA交y轴于C,交对称轴于Q,将∠CBA绕点B顺时针旋转,∠CBA的两边分别交x轴、y轴于点E、F.设点E的坐标为(m,0).
如图,二次函数y=ax2+bxc的图象经过A(4,0),D(-1,0)和B(3,3)三,.顶点为点P.作BC⊥BA交y轴于C,交对称轴于Q,将∠CBA绕点B顺时针旋转,∠CBA的两边分别交x轴、y轴于点E、F.设点E的坐标为(m,0).