题目内容
如图，三角板ABC中，∠ACB=90°，∠B=30°，BC=6，三角板绕直角顶点C逆时针旋转，当点A的对应点A/落在AB边的起始位置上时即停止转动，则点B转过的路径长为 .
2
解析试题分析：点B转过的路径长是以点C为圆心，BC为半径，旋转角度是60度，根据弧长公式
即可求得结果．
∵AC=A′C，且∠A=60°
∴△ACA′是等边三角形．
∴∠ACA′=60°
∴点B转过的路径长是：
考点：本题考查的是弧长的计算公式
点评：本题的关键是弄清所求的是那一段弧长，圆心用半径，圆心角分别是多少，然后利用弧长公式求解．
练习册系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
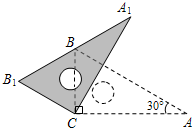如图，三角板ABC中，∠ACB=90°，∠A=30°，AB=16cm，将三角板ABC绕直角顶点C逆时针旋转，当起始位置时的点B恰好落在边A1B1上时，BB1的长是
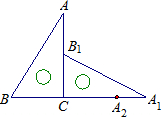如图直角三角板ABC中，∠A=30°，BC=3cm，将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置，再沿CB向左平移使点B1落在△ABC的斜边AB上，点A1平移到点A2的位置，则点A?A1?A2运动的路径长度是
应点A′落在AB边的起始位置上时即停止转动，则点B转过的路径长为
如图，三角板ABC中，∠ACB=90°，∠B=30°，BC=6．三角板绕直角顶点C逆时针旋转，当点A的对应点A'落在AB边的起始位置上时即停止转动，则点B转过的路径长为
如图，三角板ABC中，∠ACB=90°，∠B=30°，BC=6．三角板绕直角顶点C逆时针旋转，当点A的对应点A′落在AB边的起始位置上时即停止转动，则阴影部分的面积为