Question

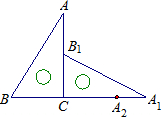如图直角三角板ABC中，∠A=30°，BC=3cm，将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A₁B₁C₁的位置，再沿CB向左平移使点B₁落在△ABC的斜边AB上，点A₁平移到点A₂的位置，则点A?A₁?A₂运动的路径长度是

 

cm．（结果用带π和根号的式子表示）

Answer 1

分析：点A由A?A₁?A₂运动的路程先是一段弧，然后是一线段，所以根据弧长公式可得．

解答：解：过B₁作B₁B₂∥BC，
根据勾股定理可得：AC=3

3

移动距离为

90×3 3 π

180

+A₁A₂
∵∠A=30°，BC=3cm
∴AB=6cm，AC=3

3

cm，
∴AB₁=（3

3

-3）cm，
∴B₁B₂=AB₁tan30°=（3-

3

）cm，
∴A₁A₂=（3-

3

）cm．
故答案为：

3 3 π

2

+3-

3

．

点评：本题主要考查了弧长公式以及勾股定理等知识，得出B₁B₂的长是解题关键．