题目内容
如图，三角板ABC中，∠ACB=90°，∠B=30°，BC=2．三角板绕直角顶点C逆时针旋转，当点A的对
应点A′落在AB边的起始位置上时即停止转动，则点B转过的路径长为分析：易得△ACA′为等边三角形，则旋转角为60°，旋转半径为2，利用弧长公式计算即可．
解答：解：∵∠ACB=90°，∠B=30°，
∴∠A=60°，
∵CA=CA′，
∴△ACA′为等边三角形，
∴∠ACA′=60°，
∴点B转过的路径长为60×π×2÷180=
π．
故答案为：
π．
∴∠A=60°，
∵CA=CA′，
∴△ACA′为等边三角形，
∴∠ACA′=60°，
∴点B转过的路径长为60×π×2÷180=
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：考查弧长的计算；得到旋转角的度数是解决本题的突破点．
练习册系列答案
相关题目
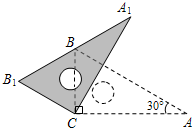如图，三角板ABC中，∠ACB=90°，∠A=30°，AB=16cm，将三角板ABC绕直角顶点C逆时针旋转，当起始位置时的点B恰好落在边A1B1上时，BB1的长是
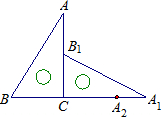如图直角三角板ABC中，∠A=30°，BC=3cm，将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置，再沿CB向左平移使点B1落在△ABC的斜边AB上，点A1平移到点A2的位置，则点A?A1?A2运动的路径长度是
如图，三角板ABC中，∠ACB=90°，∠B=30°，BC=6．三角板绕直角顶点C逆时针旋转，当点A的对应点A'落在AB边的起始位置上时即停止转动，则点B转过的路径长为
如图，三角板ABC中，∠ACB=90°，∠B=30°，BC=6．三角板绕直角顶点C逆时针旋转，当点A的对应点A′落在AB边的起始位置上时即停止转动，则阴影部分的面积为