题目内容
17．x取整数0，1，2，3，4时，不等式4x+6＞1-x与3（x-1）≤x+5都成立．分析 先求出两不等式的解集，找出组成的不等式组的解集，求出整数解即可．
解答 解：∵解不等式4x+6＞1-x得：x＞-1，
解不等式3（x-1）≤x+5得：x≤4，
∴由两不等式组成的不等式组的解集是-1＜x≤4，
∴整数x为0，1，2，3，4．
即当x取整数0，1，2，3，4时，不等式4x+6＞1-x与3（x-1）≤x+5都成立．
故答案为0，1，2，3，4．
点评 本题考查了解一元一次不等式，解一元一次不等式组，不等式组的整数解的应用，解此题的关键是求出两不等式组成的不等式组的解集，题目比较好，难度适中．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
7．在△ABC中，已知∠A=60°，BD⊥AC于点D，CE⊥AB于点E，且BD=CE，则△ABC是（ ）
| A． | 不等边三角形 | B． | 等腰三角形 | C． | 等边三角形 | D． | 直角三角形 |
8．
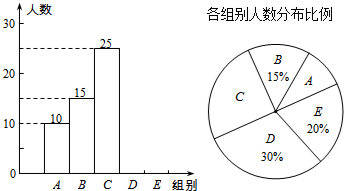某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个．随机抽取了部分学生的听写结果，绘制成如下的图表．
根据以上信息完成下列问题：
（1）统计表中的m=30，n=20，并补全条形统计图；
（2）扇形统计图中“C组”所对应的圆心角的度数是90°；
（3）已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，请你估计该校本次听写比赛不合格的学生人数．
某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个．随机抽取了部分学生的听写结果，绘制成如下的图表．| 组别 | 正常字数x | 人数 |
| A | 0≤x＜8 | 10 |
| B | 8≤x＜16 | 15 |
| C | 16≤x＜24 | 25 |
| D | 24≤x＜32 | m |
| E | 32≤x＜40 | n |
（1）统计表中的m=30，n=20，并补全条形统计图；
（2）扇形统计图中“C组”所对应的圆心角的度数是90°；
（3）已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，请你估计该校本次听写比赛不合格的学生人数．
6．在一次献爱心的捐赠活动中，某班45名同学捐款金额统计如下：
在这次活动中，该班同学捐款金额的众数和中位数分别是50，50．
| 金额（元） | 20 | 30 | 35 | 50 | 100 |
| 学生数（人） | 5 | 10 | 5 | 15 | 10 |