题目内容
已知等腰直角△ABC中,∠A=90°,直线L经过点A,过点B、C分别作BE⊥L于点E,CF⊥L与点F,若BE=3,CF=2,则EF=________.
5
分析:根据垂直的定义得∠AEB=∠CFA=90°,根据等腰直角三角形的性质得AB=AC,利用等角的余角相等得到∠ABE=∠CAF,然后根据“AAS”可判断△ABE≌△CAF,AE=CF,BE=AF,则EF=AE+AF=CF+BE=2+3=5.
解答:如图,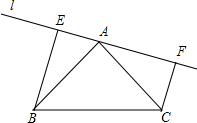
∵BE⊥L于点E,CF⊥L与点F,
∴∠AEB=∠CFA=90°,
∵△ABC为等腰直角三角形,∠A=90°,
∴AB=AC,∠EAB+∠CAF=90°,
而∠ABE+∠EAB=90°,
∴∠ABE=∠CAF,
在△ABE和△CAF中
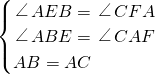 ,
,
∴△ABE≌△CAF(AAS),
∴AE=CF,BE=AF,
∵BE=3,CF=2,
∴EF=AE+AF=CF+BE=2+3=5.
故答案为5.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等腰直角三角形的性质.
分析:根据垂直的定义得∠AEB=∠CFA=90°,根据等腰直角三角形的性质得AB=AC,利用等角的余角相等得到∠ABE=∠CAF,然后根据“AAS”可判断△ABE≌△CAF,AE=CF,BE=AF,则EF=AE+AF=CF+BE=2+3=5.
解答:如图,

∵BE⊥L于点E,CF⊥L与点F,
∴∠AEB=∠CFA=90°,
∵△ABC为等腰直角三角形,∠A=90°,
∴AB=AC,∠EAB+∠CAF=90°,
而∠ABE+∠EAB=90°,
∴∠ABE=∠CAF,
在△ABE和△CAF中
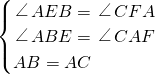 ,
,∴△ABE≌△CAF(AAS),
∴AE=CF,BE=AF,
∵BE=3,CF=2,
∴EF=AE+AF=CF+BE=2+3=5.
故答案为5.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等腰直角三角形的性质.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
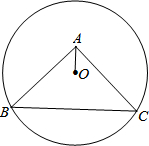 (2013•长宁区二模)如图,已知等腰直角△ABC中,∠BAC=90°,圆心O在△ABC内部,且⊙O经过B、C两点,若BC=8,AO=1,求⊙O的半径.
(2013•长宁区二模)如图,已知等腰直角△ABC中,∠BAC=90°,圆心O在△ABC内部,且⊙O经过B、C两点,若BC=8,AO=1,求⊙O的半径. 如图,已知等腰直角△ABC的直角边长和正方形DEFG的边长均为10厘米,BC与GF在同一直线上,开始时点B与点G重合,现在将△ABC以1厘米/秒的速度向右移动,直至点B与点F重合为止,设在移动过程中△ABC和正方形DEFG重叠部分的面积为y平方厘米,求出y(平方厘米)与x(厘米/秒)之间的函数关系式,并写出自变量的取值范围.
如图,已知等腰直角△ABC的直角边长和正方形DEFG的边长均为10厘米,BC与GF在同一直线上,开始时点B与点G重合,现在将△ABC以1厘米/秒的速度向右移动,直至点B与点F重合为止,设在移动过程中△ABC和正方形DEFG重叠部分的面积为y平方厘米,求出y(平方厘米)与x(厘米/秒)之间的函数关系式,并写出自变量的取值范围.