Question

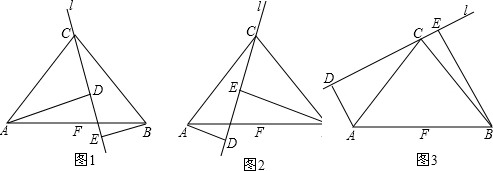
如图①，已知等腰直角△ABC中，BD为斜边上的中线，E为DC上的一点，且AG⊥BE于G，AG交BD于F．
（1）求证：AF=BE；
（2）如图②，若点E在DC的延长线上，其它条件不变，①的结论还能成立吗？若不能，请说明理由；若能，请予以证明．

Answer 1

分析：（1）首先证明AD=BD，再证明∠DAF=∠DBE，可利用ASA定理判定△AFD≌△BED，进而得到AF=BE；
（2）方法与（1）类似，证明△AFD≌△BED（AAS）可得AF=BE．

解答：证明：（1）∵△ABC是等腰三角形，BD为斜边上的中线，
∴BD=AD=

1

2

AC，∠ADB=90°，
∴∠1+∠GAD=90°，
∵AG⊥BE于G，
∴∠2+∠DBE=90°，
∵∠1=∠2，
∴∠DAF=∠DBE，
在△AFD和△BED中，

∠ADB=∠BDE AD=BD ∠DAG=∠DBE

，
∴△AFD≌△BED（SAS），
∴AF=BE；

（2）①的结论还能成立；
∵△ABC是等腰三角形，BD为斜边上的中线，
∴BD=AD=

1

2

AC，∠ADB=90°，
∴∠DBE+∠DEB=90°，
∵AG⊥BE于G，
∴∠GBF+∠F=90°，
∵∠DBE=∠GBF，
∴∠F=∠DEB，
在△AFD和△BED中，

∠DEB=∠F ∠BDF=∠ADF=90° AD=BD

，
∴△AFD≌△BED（AAS），
∴AF=BE；

点评：此题主要考查了全等三角形的判定与性质，以及直角三角形的性质，关键是掌握直角三角形斜边上的中线等于斜边的一半．