题目内容
计算:
(1)sin230°+cos245°+ sin60°•tan45°
sin60°•tan45°
(2)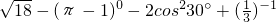
(3)
(4) •
• .
.
解:(1)原式=( )2+(
)2+( )2+
)2+ ×
× ×1
×1
= +
+ +
+
=2 ;
;
(2)原式=3 -1-2×(
-1-2×( )2+3
)2+3
=3 -1-
-1- +3
+3
=3 +
+ ;
;
(3)原式=[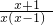 -
- ]•x
]•x
= •x
•x
=- ;
;
(4)原式= ×(-
×(- )
)
=-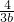 ×a2b2
×a2b2
=-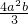
 .
.
分析:(1)根据角的三角函数值得到原式=( )2+(
)2+( )2+
)2+ ×
× ×1,然后利用二次根式的性质计算;
×1,然后利用二次根式的性质计算;
(2)根据特殊角的三角函数值、零指数幂和负整数指数幂的意义得到原式=3 -1-2×(
-1-2×( )2+3,然后利用二次根式的性质化简后合并即可;
)2+3,然后利用二次根式的性质化简后合并即可;
(3)先把括号内通分后除法运算化为乘法运算得到原式=[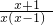 -
- ]•x=
]•x= •x,然后约分即可;
•x,然后约分即可;
(4)根据二次根式的乘除法则得到原式= ×(-
×(- )
) ,然后利用二次根式的性质化简即可.
,然后利用二次根式的性质化简即可.
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.也考查了特殊角的三角函数值、零指数幂和负整数指数幂以及分式的混合运算.
 )2+(
)2+( )2+
)2+ ×
× ×1
×1=
 +
+ +
+
=2
 ;
;(2)原式=3
 -1-2×(
-1-2×( )2+3
)2+3=3
 -1-
-1- +3
+3=3
 +
+ ;
;(3)原式=[
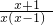 -
- ]•x
]•x=
 •x
•x=-
 ;
;(4)原式=
 ×(-
×(- )
)
=-
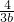 ×a2b2
×a2b2
=-
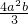
 .
.分析:(1)根据角的三角函数值得到原式=(
 )2+(
)2+( )2+
)2+ ×
× ×1,然后利用二次根式的性质计算;
×1,然后利用二次根式的性质计算;(2)根据特殊角的三角函数值、零指数幂和负整数指数幂的意义得到原式=3
 -1-2×(
-1-2×( )2+3,然后利用二次根式的性质化简后合并即可;
)2+3,然后利用二次根式的性质化简后合并即可;(3)先把括号内通分后除法运算化为乘法运算得到原式=[
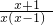 -
- ]•x=
]•x= •x,然后约分即可;
•x,然后约分即可;(4)根据二次根式的乘除法则得到原式=
 ×(-
×(- )
) ,然后利用二次根式的性质化简即可.
,然后利用二次根式的性质化简即可.点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.也考查了特殊角的三角函数值、零指数幂和负整数指数幂以及分式的混合运算.

练习册系列答案
相关题目
 cos60°=
cos60°= cos=45°=
cos=45°= cos30°=
cos30°=