题目内容
如图,A(0,
),B(-1,0),C为x轴上一点,四边形ABCD为菱形.
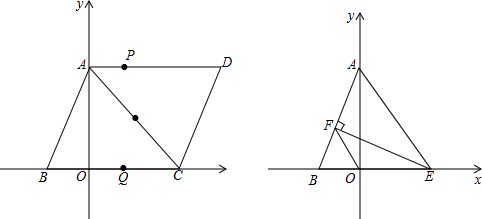
(1)求C点坐标;
(2)点O′为AC的中点,动点P、Q同时从点B出发,点P沿B→A→D方向以2cm/s的速度运动,点Q沿B→C方向以1cm/s的速度运动,设运动时间为t秒,连PQ,是否存在实数t,使PQ正好经过O′?若存在,求出t值;若不存在,说明理由;
(3)点E为x轴正半轴上一动点,当EF⊥AB于F时,求
的值.
| 3 |

(1)求C点坐标;
(2)点O′为AC的中点,动点P、Q同时从点B出发,点P沿B→A→D方向以2cm/s的速度运动,点Q沿B→C方向以1cm/s的速度运动,设运动时间为t秒,连PQ,是否存在实数t,使PQ正好经过O′?若存在,求出t值;若不存在,说明理由;
(3)点E为x轴正半轴上一动点,当EF⊥AB于F时,求
| OF |
| AE |
考点:四边形综合题,全等三角形的判定与性质,菱形的性质,相似三角形的判定与性质
专题:综合题
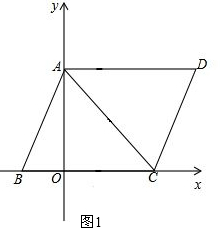
分析:(1)如图1,要求点C的坐标,只需求出OC的长,OB已知,只需求出BC即AB长,只需在Rt△AOB中运用勾股定理就可解决问题.
(2)若PQ正好经过O′,如图2,易证△AO′P≌△CO′Q,则有AP=CQ,从而建立关于t的方程,解这个方程就可解决问题.
(3如图3,易证△AOB∽△EFB,则有
=
,从而可证到△FBO∽△EBA,然后运用相似三角形的性质即可解决问题.
(2)若PQ正好经过O′,如图2,易证△AO′P≌△CO′Q,则有AP=CQ,从而建立关于t的方程,解这个方程就可解决问题.
(3如图3,易证△AOB∽△EFB,则有
| BO |
| BF |
| BA |
| BE |
解答:解:(1)如图1,
∵A(0,
),B(-1,0),
∴OA=
,OB=1.
∵∠AOB=90°,
∴AB=
=
=2.
∵四边形ABCD为菱形,
∴BC=AB=2,∴OC=BC-OB=2-1=1,
∴C点坐标为(1,0).
(2)若PQ正好经过O′,如图2.
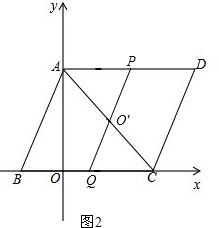
∵四边形ABCD为菱形,∴AD∥BC,
∴∠PAO′=∠QCO′,∠APO′=∠CQO′.
在△AO′P和△CO′Q中,
,
∴△AO′P≌△CO′Q,
∴AP=CQ.
由题可得:AP=2t-2,QC=BC-BQ=2-t,
则有2t-2=2-t,
解得:t=
.
∴当实数t=
时,PQ正好经过O′.
(3)如图3,
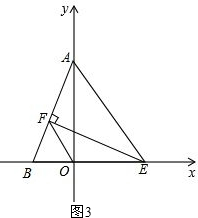
∵∠BFE=∠BOA=90°,∠ABO=∠EBF,
∴△AOB∽△EFB,
∴
=
.
∵∠FBO=∠EBA,
∴△FBO∽△EBA,
∴
=
=
.
∴
的值为
.

∵A(0,
| 3 |
∴OA=
| 3 |
∵∠AOB=90°,
∴AB=
| OA2+OB2 |
| 3+1 |
∵四边形ABCD为菱形,
∴BC=AB=2,∴OC=BC-OB=2-1=1,
∴C点坐标为(1,0).
(2)若PQ正好经过O′,如图2.

∵四边形ABCD为菱形,∴AD∥BC,
∴∠PAO′=∠QCO′,∠APO′=∠CQO′.
在△AO′P和△CO′Q中,
|
∴△AO′P≌△CO′Q,
∴AP=CQ.
由题可得:AP=2t-2,QC=BC-BQ=2-t,
则有2t-2=2-t,
解得:t=
| 4 |
| 3 |
∴当实数t=
| 4 |
| 3 |
(3)如图3,

∵∠BFE=∠BOA=90°,∠ABO=∠EBF,
∴△AOB∽△EFB,
∴
| BO |
| BF |
| BA |
| BE |
∵∠FBO=∠EBA,
∴△FBO∽△EBA,
∴
| OF |
| AE |
| OB |
| AB |
| 1 |
| 2 |
∴
| OF |
| AE |
| 1 |
| 2 |
点评:本题考查了菱形的性质、全等三角形的判定与性质、相似三角形的性质、勾股定理等知识,利用相似三角形的性质是解决第(3)小题的关键.

练习册系列答案
相关题目
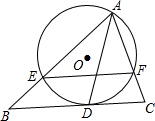 如图,直线BC与半径为2的⊙O相切于点D,A是⊙O上一点,AB交⊙O于点E,AC交⊙O于点F,BC∥EF.
如图,直线BC与半径为2的⊙O相切于点D,A是⊙O上一点,AB交⊙O于点E,AC交⊙O于点F,BC∥EF.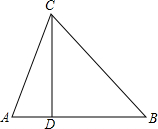 如图,已知△ABC中,AC=5,AB=6,BC=7,AB边上的高CD=3
如图,已知△ABC中,AC=5,AB=6,BC=7,AB边上的高CD=3