题目内容
16.已知二次函数y=ax2+bx+c的图象经过点A(1,0).(1)当b=2,c=-3时,求二次函数的解析式及二次函数最小值;
(2)二次函数的图象经过点B(m,e),C(3-m,e).
①求该二次函数图象的对称轴;
②若对任意实数x,函数值y都不小于$\frac{1}{4a}$-$\frac{1}{2}$,求此时二次函数的解析式.
分析 (1)利用待定系数法以及配方法即可解决问题.
(2)①根据对称性B、C关于对称轴对称,即可解决问题.
②首先求出b、c(用a表示),想办法列出不等式即可解决问题.
解答 解:(1)将b=2,c=-3代入得:y=ax2+2x-3.
将x=1,y=0代入,a+2-3=0,
∴a=1.
∴y=x2+2x-3=(x+1)2-4,
∴当x=-1时,y最小值为-4.
(2)①由题意可知:对称轴x=$\frac{m+3-m}{2}$=$\frac{3}{2}$.
②∵-$\frac{b}{2a}$=$\frac{3}{2}$,
∴b=-3a,又∵a+b+c=0,
∴c=2a,
∴y=ax2-3ax+2a
顶点纵坐标为$\frac{4ac-{b}^{2}}{4a}$=$\frac{-{a}^{2}}{4a}$,
∵函数值不小于$\frac{1}{4a}$-$\frac{1}{2}$,
∴a>0,且-$\frac{{a}^{2}}{4a}$≥$\frac{1}{4a}$-$\frac{1}{2}$,
∴a2-2a+1≤0,
∴(a-1)2≤0,
∵(a-1)2≥0,
∴a-1=0,
∴a=1.
点评 本题考查待定系数法、二次函数的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,属于中考常考题型.

练习册系列答案
相关题目
6.下列计算结果正确的是( )
| A. | a3•a3=a9 | B. | (-y)5÷(-y)3=y2 | C. | (a3)2=a5 | D. | (a+b)2=a2+b2 |
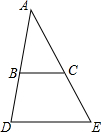 如图,已知在△ADE中,∠ABC=∠D,∠ACB=50°,求∠E.
如图,已知在△ADE中,∠ABC=∠D,∠ACB=50°,求∠E.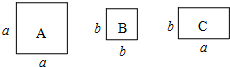 有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(a+2b)的大长方形,则需要C类卡片5张.
有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(a+2b)的大长方形,则需要C类卡片5张. 如图所示,图中的x的值是65°.
如图所示,图中的x的值是65°. 如图,用直角曲尺检查半圆形的工件,其中合格的是图乙(填“甲”、“乙”或“丙”),你的根据是90°圆周角所对的弦是直径.
如图,用直角曲尺检查半圆形的工件,其中合格的是图乙(填“甲”、“乙”或“丙”),你的根据是90°圆周角所对的弦是直径.