题目内容
8．
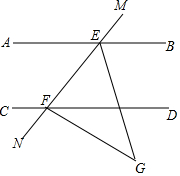如图，AB∥CD，GE=GF，∠NFG=110°，EG平分∠BEF，求∠DFG的度数．
分析 先根据等腰三角形的性质，得到∠EFG=70°=∠FEG，再根据EG平分∠BEF，即可得出∠BEM=40°，再根据AB∥CD，可得∠DFE=∠BEM=40°，最后根据∠DFG=180°-∠DFE-∠NFG进行计算即可．
解答 解：∵GE=GF，∠NFG=110°，
∴∠EFG=70°=∠FEG，
又∵EG平分∠BEF，
∴∠BEF=2∠FEG=140°，
∴∠BEM=40°，
∵AB∥CD，
∴∠DFE=∠BEM=40°，
∴∠DFG=180°-∠DFE-∠NFG=180°-40°-110°=30°．
点评 本题主要考查了平行线的性质，角平分线的定义的运用，解题时注意：两直线平行，同位角相等．
练习册系列答案
相关题目
18．
如图，已知直线m⊥n，在某平面直角坐标系中，x轴∥直线m，y轴∥直线n，点A、B的坐标分别为（-4，2），（2，-4），点A，O4，B在同一条直线上，则坐标原点为（ ）
如图，已知直线m⊥n，在某平面直角坐标系中，x轴∥直线m，y轴∥直线n，点A、B的坐标分别为（-4，2），（2，-4），点A，O4，B在同一条直线上，则坐标原点为（ ）| A． | O1 | B． | O2 | C． | O3 | D． | O4 |
16．下列方程为一元一次方程的是（ ）
| A． | x+4=4-x2 | B． | x+y=-3x | C． | $\frac{1}{2x+3}=1$ | D． | 5-$\frac{1}{3}x=\frac{2}{3}x$ |
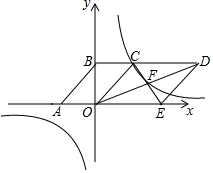如图，已知反比例函数y=$\frac{1-m}{x}$（m为常数）的图象在平面直角坐标系的第一、三象限，且经过?ABCO的顶点C，点A，B的坐标分别为（-2，0），（0，3），若点P是该反比例函数图象上的一点，且OC=OP，则满足条件的位于第三象限内P点坐标为（-3，-2）或（-2，-3）；若该反比例函数图象又经过?COED对角线的交点F，则?COED的面积为18．
17．某小组参加植树活动，全组学生的植树数量如表所示，则该小组平均每人植树7株．
| 植树数量（株） | 5 | 6 | 7 | 8 |
| 人数（人） | 1 | 1 | 2 | 3 |