题目内容
5.如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.
(1)赛道的长度是50m,甲的速度是25m/s;
(2)分别写出甲在0≤t≤20和20<t≤40时,y关于t的函数关系式:当0≤t≤20,y=-2.5t+50;当20<t≤40时,y=2.5t-50;
(3)在图2中画出乙在2分钟内的函数大致图象(用虚线画);
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了几次?2分钟时,乙距池边B1B2的距离为多少米.
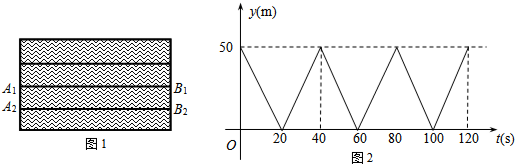
分析 (1)由函数图象可以直接得出赛道的长度为50米,由路程÷时间=速度就可以求出甲的速度.
(2)先根据图象的形状,可判断出甲在0≤t≤20和20<t≤40时,y都是t的一次函数,设出其解析式,再运用待定系数法求解;
(3)乙的速度为2m/s,由B2到达A2的路程为赛道的长度50m,根据时间=路程÷速度,即可求出乙由B2到达A2的时间为25s;乙在2分钟内可运动2个来回,每25s可从赛道一端运动到另外一端,起点在原点,据此在图2中画出乙在2分钟内的函数图象;
(4)两个图象的交点个数即为相遇次数,根据乙船在2分钟内可运动2个来回,每25s可从赛道一端运动到另外一端,所以2分钟时,乙距池边B1B2的距离为20秒所游的路程.
解答 解:(1)由图象,得
赛道的长度是:50米,
甲的速度是:50÷20=2.5m/s.
故答案为:50,25;
(2)当0≤t≤20时,设y=k1x+b1,
把(0,50),(20,0)代入得:$\left\{\begin{array}{l}{{b}_{1}=50}\\{20{k}_{1}+{b}_{1}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-2.5}\\{{b}_{1}=50}\end{array}\right.$
∴y=-2.5t+50,
当20<t≤40时,设y=k2x+b2,
把(20,0),(40,50)代入得:$\left\{\begin{array}{l}{20{k}_{2}+{b}_{2}=0}\\{40{k}_{2}+{b}_{2}=50}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=2.5}\\{{b}_{2}=-50}\end{array}\right.$
∴y=2.5t-50.
故答案为:y=-2.5t+50,y=2.5t-50.
(3)因为赛道的长度为50米,乙的速度为2米/秒,所以乙由B2到达A2的时间为25秒;
乙在2分钟内的函数图象如图5所示: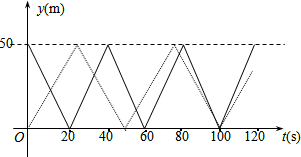
(4)从上图可知甲、乙共相遇5次.
2分钟=120秒,120-25×4=20(s),
∴2分钟时,乙距池边B1B2的距离为:20×2=40(米).
点评 本题主要考查函数模型的建立与应用,主要涉及了分段函数,以及分段函数的图象及其应用,解决本题的关键是用待定系数法求函数解析式,以及数形结合的思想与方法.

| A. | 3x-2y=4z | B. | 6xy+13=0 | C. | 3x=y-1 | D. | $\frac{1}{x}$+3y=2 |
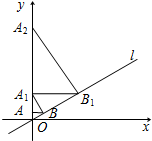 如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A5的坐标为(0,210).
如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A5的坐标为(0,210).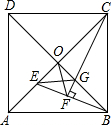 如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连接EG、OF.下列三个结论:①CE=CB;②AE=$\sqrt{2}$OE;③OF=$\frac{1}{2}$CG.其中正确的结论只有( )
如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连接EG、OF.下列三个结论:①CE=CB;②AE=$\sqrt{2}$OE;③OF=$\frac{1}{2}$CG.其中正确的结论只有( ) 如图,四边形ABCD是平行四边形,EF分别是BC、AD上的点,∠1=∠2.
如图,四边形ABCD是平行四边形,EF分别是BC、AD上的点,∠1=∠2.