题目内容
18.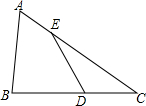 如图,D、E分别为△ABC边BC、AC上一点,证明:$\frac{{S}_{△ABC}}{{S}_{△ECD}}$=$\frac{AC•BC}{EC•CD}$.
如图,D、E分别为△ABC边BC、AC上一点,证明:$\frac{{S}_{△ABC}}{{S}_{△ECD}}$=$\frac{AC•BC}{EC•CD}$.
分析 分别过B,D作BF⊥AC于F,DG⊥AC于G,于是得到BF∥DG推出△CDG~△CBF根据相似三角形的性质得到$\frac{BF}{DG}=\frac{BC}{DC}$然后根据三角形的面积公式即可得到结论$\frac{{S}_{△ABC}}{{S}_{△ECD}}$=$\frac{\frac{1}{2}AC•BF}{\frac{1}{2}EC•DG}$=$\frac{AC•BF}{EC•DG}$=$\frac{AC•BC}{EC•CD}$.
解答  证明:分别过B,D作BF⊥AC于F,DG⊥AC于G,
证明:分别过B,D作BF⊥AC于F,DG⊥AC于G,
则BF∥DG
∴△CDG~△CBF
∴$\frac{BF}{DG}=\frac{BC}{DC}$
∴$\frac{{S}_{△ABC}}{{S}_{△ECD}}$=$\frac{\frac{1}{2}AC•BF}{\frac{1}{2}EC•DG}$=$\frac{AC•BF}{EC•DG}$=$\frac{AC•BC}{EC•CD}$.
点评 本题考查了相似三角形的判定和性质,三角形的面积,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
8.对于△ABC,下列叙述错误的是( )
| A. | 如果∠A=∠B=∠C,那么△ABC一定是锐角三角形 | |
| B. | 如果∠A=∠B+∠C,那么△ABC一定是直角三角形 | |
| C. | 如果∠A:∠B:∠C=1:3:5,那么△ABC是钝角三角形 | |
| D. | 如果∠A=40°,∠B=3∠C,那么△ABC是锐角三角形 |
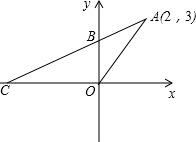 如图所示,已知一次函数y=kx+b的图象经过点A(2,3)和点B(0,2),且与x轴相交于点C.
如图所示,已知一次函数y=kx+b的图象经过点A(2,3)和点B(0,2),且与x轴相交于点C.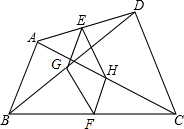 如图,任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,给四边形ABCD添加一个条件,使四边形EGFH是菱形,你添加的一个条件是AB=CD.请加以说明.
如图,任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,给四边形ABCD添加一个条件,使四边形EGFH是菱形,你添加的一个条件是AB=CD.请加以说明.