题目内容
9.(2+1)(22+1)(24+1)…(232+1)+1的个位数字是6.分析 原式乘以2-1,再依次根据平方差公式进行计算,求出结果,即可得出答案.
解答 解:原式=(2-1)(2+1)(22+1)(24+1)…(232+1)+1
=(22-1)(22+1)(24+1)…(232+1)+1
=(24-1)(24+1)…(232+1)+1的
=(2+1)(22+1)(24+1)…(232+1)+1的
=(232-1)(232+1)+1
=264-1+1
=264,
∵21=2,22=4,23=8,24=16,25=32,26=64,…,64÷4=16,
∴264的个位数字是6,
故答案为:6.
点评 本题考查了平方差公式的应用,能灵活运用平方差公式进行计算是解此题的关键,注意:(a+b)(a-b)=a2-b2.

练习册系列答案
相关题目
4.已知多项式(x2-mx+1)(x-2)的积中不含x的二次项系数,则m的值是( )
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
19.下列各数中,不是无理数的是( )
| A. | $\sqrt{7}$ | B. | $\root{3}{125}$ | ||
| C. | π | D. | 0.15115111511115… |
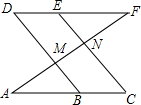 如图,已知DF∥AC,∠C=∠D,求证:∠AMB=∠ANC.
如图,已知DF∥AC,∠C=∠D,求证:∠AMB=∠ANC.