题目内容
如图，E点在AB上，AC=AD，BC=BD，则全等三角形的对数有（ ）分析：由AC=AD，BC=BD，加上公共边AB相等，利用SSS得出三角形ABD与三角形ABC全等，利用全等三角形的对应角相等得到∠DAB=∠CAB，∠DBA=∠CBA，再利用SAS得出三角形ADE与三角形ACE全等，三角形DBE与三角形CBE全等．
解答：解：全等三角形的对数有3对，分别为△ABD≌△ABC；△ADE≌△ACE；△DBE≌△CBE，
理由为：在△ABD与△ABC中，
，
∴△ABD≌△ABC（SSS），
∴∠DAB=∠CAB，∠DBA=∠CBA，
在△ADE和△ACE中，
，
∴△ADE≌△ACE（SAS）；
在△DBE和△CBE中，
，
∴△DBE≌△CBE（SAS）．
故选C
理由为：在△ABD与△ABC中，
|
∴△ABD≌△ABC（SSS），
∴∠DAB=∠CAB，∠DBA=∠CBA，
在△ADE和△ACE中，
|
∴△ADE≌△ACE（SAS）；
在△DBE和△CBE中，
|
∴△DBE≌△CBE（SAS）．
故选C
点评：此题考查了全等三角形的判定，熟练掌握全等三角形的判定方法是解本题的关键．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
（1）在如图所示的方格纸中，经过线段AB外一点C，不用量角器与三角尺，仅用直尺，画线段AB的垂线和平行线．
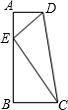如图，在梯形ABCD中，AD∥BC，BC⊥AB，AD=3，BC=4，E点在AB上，且AE=2，∠CED=90°．
如图，两块完全相同的含30°角的直角三角板叠放在一起，D点在AB上，设DE交AC于点F，有下列四个结论：①AC⊥DE；②AF=CF；③EF=3DF；④
=CE·CD．