题目内容
3．在下列各数$\sqrt{8}$；0；3π；$\root{3}{125}$；$\frac{22}{7}$；1.1010010001…，无理数的个数是（ ）| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
解答 解：$\sqrt{8}$；3π；1.1010010001…是无理数，
故选：C．
点评 此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图，在△ABC中，∠C=90°，AD平分∠CAB，交BC于点D，CD=15cm，则点D到AB的距离是15cm．
14．对于任意不相等的两个实数a、b，定义运算※如下：a※b=$\frac{\sqrt{a+b}}{a-b}$；例如3※2=$\frac{\sqrt{3+2}}{3-2}$=$\sqrt{5}$．那么5※7等于（ ）
| A． | $-\sqrt{3}$ | B． | -4 | C． | $-2\sqrt{3}$ | D． | -3 |
如图是一数值转换机，若输入的x为-4，则输出的结果为10．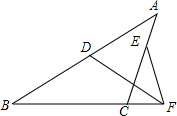
如图，在△ABC中，F为BC延长线一点，D为AB上一点，且DB=DF，E为AC上一点，且EC=EF，∠A=40°，∠DFE的度数为（ ）
15．若函数y=$\frac{x-2}{{x}^{2}-1}$的函数值为0，则自变量x的值为（ ）
| A． | 2 | B． | -1 | C． | ±1 | D． | 1 |
读语句画图，再填空，如图：