Question

【题目】如图，在等腰直角三角形中，，点是的中点，将绕点旋转至的位置，使，其中点的运动路径为弧，连接，则图中阴影部分的面积为_______．

Answer 1

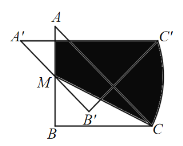
【答案】．

【解析】

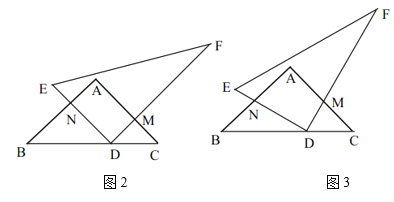
连接MC'，由可证得△A'MH为等腰直角三角形，进而可求得A'H，CH，MH的长，再利用旋转角相等求得∠CMC'的度数，最后利用扇形的面积公式计算即可．

解：如图，连接MC'，

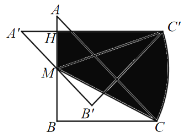
∵在等腰直角三角形中，，点是的中点，

∴∠A=45°，AM=BM=2，AC=，

∵旋转，

∴∠A'=∠A=45°，A'C'=AC=，A'M=AM=2，

又∵，

∴△A'MH为等腰直角三角形，

∴A'H=MH=A'M=，∠A'MH=45°，

∴C'H=A'C'－A'H=，

∴S△MHC'=

在Rt△MHC'中，MC'=，

又∵∠C'MC=∠A'MH=45°，

∴S扇形CMC'=，

∴阴影部分面积为S△MHC'+S扇形CMC'=．