题目内容
12.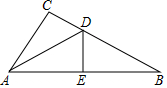 如图,在△ABC中,∠ACB=108°,AD平分∠CAB交BC于点D,DE垂直平分AB交AB于点E.
如图,在△ABC中,∠ACB=108°,AD平分∠CAB交BC于点D,DE垂直平分AB交AB于点E.(1)求∠B的度数;
(2)若AC=22,CD=13,DE=12,求△ACD的周长.
分析 (1)根据三角形的内角和得到∠CAB+∠B=72°,根据角平分线的定义得到∠DAE=∠CAE,根据线段垂直平分线的性质得到AD=BD,于是得到∠DAE=∠B,即可得到结论;
(2)过D作DF⊥AC于F,根据角平分线的性质得到DF=DE=12,根据勾股定理即可得到结论.
解答 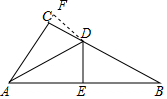 解:(1)∵∠ACB=108°,
解:(1)∵∠ACB=108°,
∴∠CAB+∠B=72°,
∵AD平分∠CAB交BC于点D,
∴∠DAE=∠CAE,
∵DE垂直平分AB,
∴AD=BD,
∴∠DAE=∠B,
∴∠CAB=2∠B,
∴∠B=24°,
(2)过D作DF⊥AC于F,
∵AD平分∠CAB交BC于点D,DE⊥AB,
∴DF=DE=12,
∴CF=$\sqrt{C{D}^{2}-D{F}^{2}}$=5,
∴AF=AC+CF=27,
∴AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=3$\sqrt{97}$,
∴△ACD的周长=AD+AC+CD=35+3$\sqrt{97}$.
点评 本题考查了线段的垂直平分线的性质,等腰三角形的性质,勾股定理,正确的识别图形是解题的关键.

练习册系列答案
相关题目
2.在南水北调正是通水之前,某学校在征得上级教育主管部分的批准后,计划组织本校七八年级学生自愿参加某旅行社的“渠首一日游”活动,此项活动的收费标准如下:
已知该校七年级报名参加的学生人数多于100人,八年级报名参加的学生人数少于100人,经核算,若七八年级分别组团共需花费20800元,若七八年级联合组团只需花费18000元.
(1)七八年级报名参加旅游的学生人数之和超过200人么?为什么?
(2)七八年级报名参加旅游的学生各有多少人?
| 人数m | 0<m≤100 | 100<m≤200 | m>200 |
| 收费标准(元/人) | 90 | 85 | 75 |
(1)七八年级报名参加旅游的学生人数之和超过200人么?为什么?
(2)七八年级报名参加旅游的学生各有多少人?
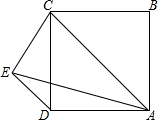 在正方形ABCD中,AC为对角线,DE平行于AC,AE=AC,求∠CED的度数.
在正方形ABCD中,AC为对角线,DE平行于AC,AE=AC,求∠CED的度数.