题目内容
1. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠CDB=30°,CD=2$\sqrt{3}$,求图中阴影部分的面积.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠CDB=30°,CD=2$\sqrt{3}$,求图中阴影部分的面积.
分析 根据AB是⊙O的直径,弦CD⊥AB,由垂径定理得CE=DE,再根据三角函数的定义即可得出OC,可证明Rt△COE≌Rt△DBE,即可得出S阴影=S扇形OBC.
解答 解:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=$\sqrt{3}$.
∵∠CDB=30°,
∴∠COE=60°,
在Rt△OEC中,OC=$\frac{OE}{sin60°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,
∵CE=DE,
∠COE=∠DBE=60°
∴Rt△COE≌Rt△DBE,
∴S阴影=S扇形OBC=$\frac{1}{6}$π×OC2=$\frac{1}{6}$π×4=$\frac{2}{3}$π.
点评 本题考查了垂径定理定理,扇形的面积,三角形的面积的应用,解此题的关键是求出扇形和三角形的面积,题目比较典型,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图,?OABC的顶点C在x轴的正半轴上,顶点A、B在第一象限内,且点A的横坐标为2,对角线AC与OB交于点D,若反比例函数y=$\frac{10}{x}$的图象经过点A与点D,则?OABC的面积为( )
如图,?OABC的顶点C在x轴的正半轴上,顶点A、B在第一象限内,且点A的横坐标为2,对角线AC与OB交于点D,若反比例函数y=$\frac{10}{x}$的图象经过点A与点D,则?OABC的面积为( )
 如图,?OABC的顶点C在x轴的正半轴上,顶点A、B在第一象限内,且点A的横坐标为2,对角线AC与OB交于点D,若反比例函数y=$\frac{10}{x}$的图象经过点A与点D,则?OABC的面积为( )
如图,?OABC的顶点C在x轴的正半轴上,顶点A、B在第一象限内,且点A的横坐标为2,对角线AC与OB交于点D,若反比例函数y=$\frac{10}{x}$的图象经过点A与点D,则?OABC的面积为( )| A. | 30 | B. | 24 | C. | 20 | D. | 16 |
6.若代数式$\sqrt{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x<2 | B. | x>2 | C. | x≥2 | D. | x≤2 |
10.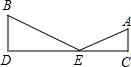 如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )
如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )
 如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )
如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )| A. | 20cm | B. | 30cm | C. | 15cm | D. | 35cm |
11.下列计算结果正确的是( )
| A. | 2a3+a3=3a6 | B. | (-a)2•a3=-a6 | C. | (-$\frac{1}{2}$)-2=4 | D. | (-2)0=-1 |
 如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为( )
如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为( )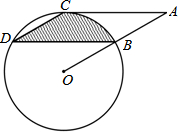 如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=4$\sqrt{3}$,则由弦CD,BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π.(结果保留π)
如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=4$\sqrt{3}$,则由弦CD,BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π.(结果保留π)