题目内容
4.若不等式(2a-b)x+3a-4b<0的解集是x>$\frac{9}{4}$,则不等式(a-4b)x+2a-3b>0的解集是x>-$\frac{16}{57}$.分析 根据(2a-b)x+3a-4b<0的解集是x>$\frac{9}{4}$,可以得到a与b的关系以及b的正负,从而可以得到所求不等式的解集.
解答 解:∵(2a-b)x+3a-4b<0的解集为x>$\frac{9}{4}$,
∴-$\frac{3a-4b}{2a-b}$=$\frac{9}{4}$且2a-b<0,
解得,a=$\frac{5}{6}$b且a<$\frac{b}{2}$,
则b<0,
∴(a-4b)x+2a-3b>0,
解得,x>-$\frac{16}{57}$,
故答案为:x>-$\frac{16}{57}$.
点评 本题考查解一元一次不等式,解答本题的关键是明确解一元一次不等式的方法,利用不等式的性质解答.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
1. 如图,a∥b,把三角板的直角顶点放在直线a上,∠1=50°,则∠2的度数为( )
如图,a∥b,把三角板的直角顶点放在直线a上,∠1=50°,则∠2的度数为( )
 如图,a∥b,把三角板的直角顶点放在直线a上,∠1=50°,则∠2的度数为( )
如图,a∥b,把三角板的直角顶点放在直线a上,∠1=50°,则∠2的度数为( )| A. | 40° | B. | 50° | C. | 55° | D. | 60° |
2. 如图,数轴上表示的是以下哪个不等式组的解集( )
如图,数轴上表示的是以下哪个不等式组的解集( )
 如图,数轴上表示的是以下哪个不等式组的解集( )
如图,数轴上表示的是以下哪个不等式组的解集( )| A. | $\left\{\begin{array}{l}{x>2}\\{x≥-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<2}\\{x≤-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥2}\\{x>-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≤2}\\{x<-1}\end{array}\right.$ |
13.一根头发丝的半径约为0.00003米,0.00003用科学记数法表示为( )
| A. | 3×10-4 | B. | 3×10-5 | C. | 3×10-6 | D. | 0.3×10-4 |
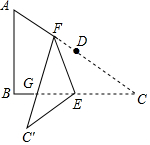 如图,在Rr△ABC中,∠B=90°,AB=3,BC=4,点D、E分别是AC,BC的中点,点F是AD上一点,将△CEF沿EF折叠得△C′EF,C′F交BC于点G.当△CFG与△ABC相似时,CF的长为4或2.8.
如图,在Rr△ABC中,∠B=90°,AB=3,BC=4,点D、E分别是AC,BC的中点,点F是AD上一点,将△CEF沿EF折叠得△C′EF,C′F交BC于点G.当△CFG与△ABC相似时,CF的长为4或2.8.