题目内容
 在△ABC中,D为BC的中点,AB=5,AD=6,AC=13.试判断AD与AB的位置关系.
在△ABC中,D为BC的中点,AB=5,AD=6,AC=13.试判断AD与AB的位置关系.考点:勾股定理的逆定理,全等三角形的判定与性质
专题:
分析:延长AD至E,使得AD=DE,连接BE,可根据SAS证明△ADC≌△EDB,然后根据勾股定理,可以得出垂直.
解答: 解:延长AD至E,使得AD=DE,连接BE,
解:延长AD至E,使得AD=DE,连接BE,
∵D为BC的中点,
∴BD=CD,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
∴EB=AC=13,
∵AD=6,
∴AE=12,
∵52+122=132,
∴AB2+AE2=EB2,
∴∠BAE=90°,
∴AD⊥AB.
 解:延长AD至E,使得AD=DE,连接BE,
解:延长AD至E,使得AD=DE,连接BE,∵D为BC的中点,
∴BD=CD,
在△ADC和△EDB中,
|
∴△ADC≌△EDB(SAS),
∴EB=AC=13,
∵AD=6,
∴AE=12,
∵52+122=132,
∴AB2+AE2=EB2,
∴∠BAE=90°,
∴AD⊥AB.
点评:此题主要考查了勾股定理逆定理,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
北海市全市常住人口为1539300人,用科学记数法表示1539300是( )
| A、15393×10-2 |
| B、15393×102 |
| C、0.15393×107 |
| D、1.5393×106 |
 线段AD=12cm,线段AC=BD=8cm,E、F分别是线段AB、CD中点,求EF.
线段AD=12cm,线段AC=BD=8cm,E、F分别是线段AB、CD中点,求EF.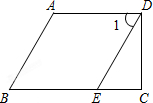 如图,AD∥BC,∠1=∠B.
如图,AD∥BC,∠1=∠B.