题目内容
13.若$\sqrt{{a}^{2}-3a+1}$+b2-2b+1=0,则a2+$\frac{1}{{a}^{2}}$+|b|=9.分析 利用非负数的性质可以求得a2+1=3a,b的值,然后将它们代入整理后的所求的代数式进行求值即可.
解答 解:由$\sqrt{{a}^{2}-3a+1}$+b2-2b+1=0,得
$\sqrt{{a}^{2}-3a+1}$+(b-1)2=0,
∴a2-3a+1=0,b-1=0.
∴a2+1=3a,b=1,
∴a+$\frac{1}{a}$=$\frac{{a}^{2}+1}{a}$=$\frac{3a}{a}$=3
∴a2+$\frac{1}{{a}^{2}}$+|b|=a2+$\frac{1}{{a}^{2}}$+1=(a+$\frac{1}{a}$)2=32=9.
故答案是:9.
点评 本题考查了配方法的应用,非负数的性质.解题时利用了“整体代入”的思想,其中分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式.

练习册系列答案
相关题目
5.下列各组二次根式化成最简二次根式后的被开方数完全相同的是( )
| A. | $\sqrt{ab}$与$\sqrt{a{b}^{2}}$ | B. | $\sqrt{mn}$与$\sqrt{\frac{1}{m}+\frac{1}{n}}$ | ||
| C. | $\sqrt{{m}^{2}+{n}^{2}}$与$\sqrt{{m}^{2}-{n}^{2}}$ | D. | $\sqrt{\frac{8}{9}{a}^{3}{b}^{2}}$与$\sqrt{\frac{9}{2}{a}^{3}{b}^{4}}$ |
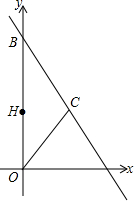 如图,在平面直角坐标系中,直线AB交x轴的正半轴于点A,交y轴正半轴于点B,点C在直线AB上,OC=OA,且OA、OB的长(OB>OA)是方程x2-15x+50=0的根.
如图,在平面直角坐标系中,直线AB交x轴的正半轴于点A,交y轴正半轴于点B,点C在直线AB上,OC=OA,且OA、OB的长(OB>OA)是方程x2-15x+50=0的根.