题目内容
直线y=kx+b与反比例函数y=
的图象相交于点A、点B,其中点A的坐标为(-2,4),点B的横坐标为4,则不等式kx+b-
>0的解集为
| m |
| x |
| m |
| x |
x<-2或0<x<4
x<-2或0<x<4
.分析:先根据点A的坐标可以求出反比例函数的解析式,再由点B的横坐标为4求出B的坐标,求出直线的解析式,求出直线与双曲线的交点坐标就可以得出结论.
解答:解:A的坐标为(-2,4)在y=
上,
∴4=-
,
∴m=-8,
∴y=-
,
当x=4时.y=-2,
∴B(4,-2),
∴
,
∴
.
∴一次函数的解析式为:y=-x+2.
∵kx+b-
>0,
∴kx+b>
,
由函数的交点坐标为:x<-2或0<x<4,
故答案为:x<-2或0<x<4.
| m |
| x |
∴4=-
| m |
| 2 |
∴m=-8,
∴y=-
| 8 |
| x |
当x=4时.y=-2,
∴B(4,-2),
∴
|
∴
|
∴一次函数的解析式为:y=-x+2.
∵kx+b-
| m |
| x |
∴kx+b>
| m |
| x |
由函数的交点坐标为:x<-2或0<x<4,
故答案为:x<-2或0<x<4.
点评:本题考查了用待定系数法求一次函数解析式的运用和反比例函数与一次函数的交点坐标的运用及不等式解集与函数图象的关系.是一道数形结合试题.

练习册系列答案
相关题目
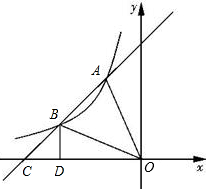 点C,过B作BD⊥x轴,且S△OBD=4,其中点A的坐标为(n,4),点B的坐标为(-4,m)
点C,过B作BD⊥x轴,且S△OBD=4,其中点A的坐标为(n,4),点B的坐标为(-4,m) (2012•宁夏)直线
(2012•宁夏)直线 (2013•沛县一模)如图,直线y=kx+b与反比例函数
(2013•沛县一模)如图,直线y=kx+b与反比例函数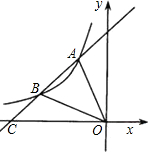 如图,直线y=kx+b与反比例函数y=
如图,直线y=kx+b与反比例函数y= 如图,直线y=kx+b与反比例函数
如图,直线y=kx+b与反比例函数