Question

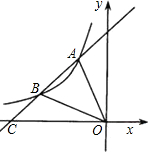如图，直线y=kx+b与反比例函数y=

k′

x

（x＜0）的图象相交于点A、点B，与x轴交于点C，其中点A的坐标为（-2，4），点B的横坐标为-4．
（1）试确定反比例函数的关系式；
（2）求△AOC的面积．

Answer 1

分析：根据A的坐标为（-2，4），先求出k′=-8，再根据反比例函数求出B点坐标，从而利用待定系数法求一次函数的解析式为y=x+6，求出直线与x轴的交点坐标后，即可求出S_△AOC=

1

2

CO•y_A=

1

2

×6×4=12．

解答：解：（1）∵点A（-2，4）在反比例函数图象上
∴4=

k′

-2

∴k′=-8，（1分）
∴反比例函数解析式为y=

-8

x

；（2分）

（2）∵B点的横坐标为-4，
∴y=-

8

-4

，
∴y=2，
∴B（-4，2）（3分）
∵点A（-2，4）、点B（-4，2）在直线y=kx+b上
∴4=-2k+b
2=-4k+b
解得k=1
b=6
∴直线AB为y=x+6（4分）
与x轴的交点坐标C（-6，0）
∴S_△AOC=

1

2

CO•y_A=

1

2

×6×4=12．（6分）

点评：主要考查了用待定系数法求函数解析式和反比例函数y=

k

x

中k的几何意义，这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=

1

2

|k|．