题目内容
 如图,直线y=kx+b与反比例函数y=
如图,直线y=kx+b与反比例函数y=| k′ | x |
(1)试确定反比例函数的关系式;
(2)试确定直线AB的解析式;
(3)求△AOB的面积.
分析:(1)根据S△OBD=4,可求出k的值,继而求出反比例函数的解析式;
(2)将A和B点的坐标代入一次函数的关系式求出即可;
(3)求出直线与x轴的交点坐标后,即可求出S△AOC=
CO•yA和S△BOC=
CO•yB.继而求出△AOB的面积.
(2)将A和B点的坐标代入一次函数的关系式求出即可;
(3)求出直线与x轴的交点坐标后,即可求出S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵点A的坐标为(-2,3),
∴xy=-6,即k=-6,
∴反比例函数的解析式为:y=-
,
(2)∵点B的横坐标为-3,
∴y=-
=2,
∴B点的坐标为:(-3,2),
∵设点A(-2,3)、点B(-3,2)在直线y=kx+b上,
,
解得:
.
∴直线AB解析式为:y=x+5;
(3)∵直线AB与x轴的交点坐标C(-5,0),
∴S△AOC=
CO•yA=
×5×3=7.5,
又∵S△BOC=
CO•yB=
×5×2=5,
∴S△AOB=S△AOC-S△BOC=2.5.
∴xy=-6,即k=-6,
∴反比例函数的解析式为:y=-
| 6 |
| x |
(2)∵点B的横坐标为-3,
∴y=-
| 6 |
| -3 |
∴B点的坐标为:(-3,2),
∵设点A(-2,3)、点B(-3,2)在直线y=kx+b上,
|

解得:
|
∴直线AB解析式为:y=x+5;
(3)∵直线AB与x轴的交点坐标C(-5,0),
∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AOB=S△AOC-S△BOC=2.5.
点评:此题主要考查了用待定系数法求函数解析式和反比例函数 y=
中k的几何意义,这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|.
| k |
| x |
| 1 |
| 2 |

练习册系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
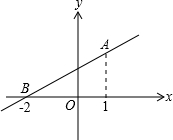 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为