题目内容
某反比例函数的图象经过点(-2,3),则此函数图象特经过点( )
| A、(2,-3) |
| B、(-3,-3) |
| C、(2,3) |
| D、(-4,6) |
考点:反比例函数图象上点的坐标特征
专题:计算题
分析:设反比例函数y=
(k为常数,k≠0),由于反比例函数的图象经过点(-2,3),则k=-6,然后根据反比例函数图象上点的坐标特征分别进行判断.
| k |
| x |
解答:解:设反比例函数y=
(k为常数,k≠0),
∵反比例函数的图象经过点(-2,3),
∴k=-2×3=-6,
而2×(-3)=-6,(-3)×(-3)=9,2×3=6,-4×6=-24,
∴点(2,-3)在反比例函数y=-
的图象上.
故选A.
| k |
| x |
∵反比例函数的图象经过点(-2,3),
∴k=-2×3=-6,
而2×(-3)=-6,(-3)×(-3)=9,2×3=6,-4×6=-24,
∴点(2,-3)在反比例函数y=-
| 6 |
| x |
故选A.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
| k |
| x |

练习册系列答案
相关题目
 实数a、b在数轴上的位置如图所示,则
实数a、b在数轴上的位置如图所示,则| (a+b)2 |
| A、2a+b | B、b |
| C、-2a | D、-b |
[-(-x)3]5=( )
| A、x15 |
| B、-x15 |
| C、x8 |
| D、-x8 |
计算:50×6-1=( )
A、
| ||
| B、0 | ||
| C、5 | ||
| D、不能确定 |
(a+b-c)(a-b-c)的计算结果是( )
| A、a2+b2-c2 |
| B、a2-b2+c2 |
| C、a2-2ab+b2-c2 |
| D、a2-2ac+c2-b2 |
等腰直角三角形斜边为10,则它的直角边为( )
A、5
| ||
B、4
| ||
C、2
| ||
D、2
|
下列几种比较数的大小的方法:①倒数大的反而小;②绝对值大的反而小;③平方大的就大;④两数的商大于1时,被除数就大.其中正确的方法有( )
| A、0种 | B、1种 | C、2种 | D、3种 |
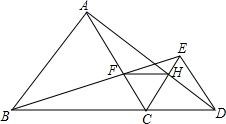 如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,求证:FH∥BD.
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,求证:FH∥BD.