题目内容
19.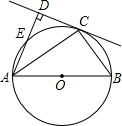 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D
如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D(1)求证:AC平分∠DAB;
(2)若∠B=60°,CD=2$\sqrt{3}$,求AD的长.
分析 (1)连接OC,由切线的性质可知:∠OCD=90°,从而可知OC∥AD,由于OC=OA,从而可证明AC平分∠DAB;
(2)由于∠B=60°,所以∠CAB=30°,所以∠DAC=30°,从而可求出AD的长度.
解答 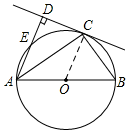 解:(1)连接OC,
解:(1)连接OC,
∵CD与⊙O相切,
∴∠OCD=90°,
∵∠ADC=90°,
∴OC∥AD,
∴∠ACO=∠DAC,
∵OC=OA,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
∴AC平分∠DAB,
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=60°,
∴∠CAO=30°,
由(1)可知:∠DAC=∠CAO=30°,
在Rt△ADC中,
tan30°=$\frac{CD}{AD}$,CD=2$\sqrt{3}$
∴AD=6
点评 本题考查圆的综合问题,涉及切线的性质,角平分线的判定,圆周角定理,锐角三角函数等知识,综合程度较高,属于中等题型.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
7.要使(x2+ax+1)(x-2)的结果中不含x2项,则a为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
14.与$\sqrt{5}$可以合并的二次根式是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{15}$ | C. | $\sqrt{20}$ | D. | $\sqrt{25}$ |
11.下列说法错误的是( )
| A. | 平移和旋转都不改变图形的形状和大小 | |
| B. | 成中心对称的两个图形中,对应点连线的中点是对称中心 | |
| C. | 在平移和旋转图形的过程中,对应角相等,对应线段相等且平行 | |
| D. | 一个图形和它经过旋转后所得的图形中,对应点到旋转中心的距离相等 |
 如图,点P是⊙O外一点,过点P作⊙O的切线PA,切点为A,连接PO,延长PO交⊙O于点B,若∠P=30°,PA=3$\sqrt{3}$,则弧AB的长为2π.
如图,点P是⊙O外一点,过点P作⊙O的切线PA,切点为A,连接PO,延长PO交⊙O于点B,若∠P=30°,PA=3$\sqrt{3}$,则弧AB的长为2π.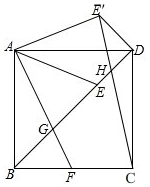 如图,正方形ABCD中,F为BC边上的中点,连接AF交对角线BD于G,在BD上截BE=BA,连接AE,将△ADE沿AD翻折得△ADE′,连接E′C交BD于H,若BG=2,则四边形AGHE′的面积是$\frac{60}{7}$-$\frac{9}{14}\sqrt{2}$.
如图,正方形ABCD中,F为BC边上的中点,连接AF交对角线BD于G,在BD上截BE=BA,连接AE,将△ADE沿AD翻折得△ADE′,连接E′C交BD于H,若BG=2,则四边形AGHE′的面积是$\frac{60}{7}$-$\frac{9}{14}\sqrt{2}$.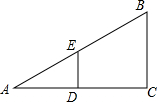 如图,在Rt△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC,交AB于点E,交AC于点D,则DE的长为( )
如图,在Rt△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC,交AB于点E,交AC于点D,则DE的长为( )