Question

13．如图，已知点P是⊙O外一点，PO交圆O于点C，OC=2，AB⊥OC，劣弧AB的度数为120°，连接PB．
（1）求证：OC=BC；
（2）当PB的长是多少时，PB是⊙O的切线？写出证明过程．

Answer 1

分析 （1）根据垂径定理得OC平分劣弧AB，则劣弧AC和劣弧BC的度数为60°，则利用圆心角的度数等于它所对弧的度数得∠COB=60°，连接OB，如图，易证得△OBC是等边三角形，所以BC=OC；
（2）由△OBC是等边三角形，则BC=OC=OB=2，∠BOP=60°，所以当∠P=30°时，∠OBP=90°，则根据切线的判定定理可判断此时PB是⊙O的切线，利用含30度的直角三角形三边的关系得到PB=$\sqrt{3}$OB=2$\sqrt{3}$，即当PB=2$\sqrt{3}$时，PB是⊙O的切线．

解答 （1）证明：∵AB⊥OC，
∴OC平分劣弧AB，
∵劣弧AB的度数为120°，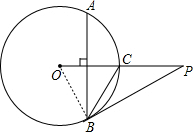
∴劣弧AC和劣弧BC的度数为60°，
即∠COB=60°，
连接OB，如图，
∵OC=OB，∠COB=60°，
∴△OBC是等边三角形，
∴BC=OC；
（2）当PB=2$\sqrt{3}$时，PB是⊙O的切线． 
证明如下：∵△OBC是等边三角形，
∴BC=OC=OB=2，∠BOP=60°，
当∠P=30°时，∠OBP=90°，
∴OB⊥PB，
∴此时PB是⊙O的切线，
∴PB=$\sqrt{3}$OB=2$\sqrt{3}$．．

点评 本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．记住含30度的直角三角形三边的关系．