题目内容
14.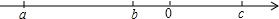 已知有理数a、b.c在数轴上的位置如图所示.
已知有理数a、b.c在数轴上的位置如图所示.(1)判断下列各式的符号:a-b,b-c,c-a;
(2)若|a|=2.|b|=$\frac{1}{2}$.|c|=1.试比较c-b与b-a之间的大小关系.
分析 根据a、b、c在数轴上的位置可得a<b<0<c.
(1)根据有理数的加减运算方法判断即可;
(2)根据绝对值的意义和在数轴上的位置,确定a、b、c的数值,计算比较即可.
解答 解:由数轴可知:a<b<0<c.
(1)a-b<0,b-c<0,c-a>0;
(2)∵|a|=2,|b|=$\frac{1}{2}$,|c|=1,a<b<0<c,
∴a=-2,b=-$\frac{1}{2}$,c=1,
∴c-b=1$\frac{1}{2}$,b-a=1$\frac{1}{2}$,
∴c-b=b-a.
点评 此题考查数轴,绝对值的意义,解答本题的关键是根据图示判断出a<b<0<c,并且掌握绝对值的化简.

练习册系列答案
相关题目
6.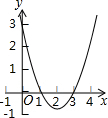 二次函数y=x2-4x+3的图象如图所示,利用图象可判断方程x2-4x+$\frac{10}{3}$=0较大的解所在的范围是( )
二次函数y=x2-4x+3的图象如图所示,利用图象可判断方程x2-4x+$\frac{10}{3}$=0较大的解所在的范围是( )
 二次函数y=x2-4x+3的图象如图所示,利用图象可判断方程x2-4x+$\frac{10}{3}$=0较大的解所在的范围是( )
二次函数y=x2-4x+3的图象如图所示,利用图象可判断方程x2-4x+$\frac{10}{3}$=0较大的解所在的范围是( )| A. | 0<x<1 | B. | 1<x<2 | C. | 2<x<3 | D. | x>3 |
 如图,在等腰直角三角形ABC中,AD是斜边BC上的高,则AD=BD=CD,请说明理由.
如图,在等腰直角三角形ABC中,AD是斜边BC上的高,则AD=BD=CD,请说明理由.