题目内容
16.阅读下面的材料:如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)=$\frac{2}{x}$(x>0)是减函数.
证明:假设x1<x2,且x1>0,x2>0
f(x1)-f(x2)=$\frac{2}{{x}_{1}}$-$\frac{2}{{x}_{2}}$=$\frac{2{x}_{2}-2{x}_{1}}{{x}_{1}{x}_{2}}$=$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}{x}_{2}}$
∵x1<x2,且x1>0,x2>0
∴x2-x1>0,x1x2>0
∴$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}{x}_{2}}$>0,即f(x1)-f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)=$\frac{2}{x}$(x>0)是减函数.
根据以上材料,解答下面的问题:
(1)函数f(x)=$\frac{1}{{x}^{2}}$(x>0),f(1)=$\frac{1}{{1}^{2}}$=1,f(2)=$\frac{1}{{2}^{2}}$=$\frac{1}{4}$.
计算:f(3)=$\frac{1}{9}$,f(4)=$\frac{1}{16}$,猜想f(x)=$\frac{1}{{x}^{2}}$(x>0)是减函数(填“增”或“减”);
(2)请仿照材料中的例题证明你的猜想.
分析 (1)根据题意把x=3,x=4代入,再比较其大小即可;
(2)假设x1<x2,且x1>0,x2>0,再作差比较即可.
解答 (1)解:∵f(x)=$\frac{1}{{x}^{2}}$(x>0),f(1)=$\frac{1}{{1}^{2}}$=1,f(2)=$\frac{1}{{2}^{2}}$=$\frac{1}{4}$,
∴f(3)=$\frac{1}{{3}^{2}}$=$\frac{1}{9}$,f(4)=$\frac{1}{{4}^{2}}$=$\frac{1}{16}$,
∵$\frac{1}{9}$>$\frac{1}{16}$,
∴猜想f(x)=$\frac{1}{{x}^{2}}$(x>0)是减函数.
故答案为:$\frac{1}{9}$,$\frac{1}{16}$,减;
(2)证明:假设x1<x2,且x1>0,x2>0
f(x1)-f(x2)=$\frac{1}{{{x}_{1}}^{2}}$-$\frac{1}{{{x}_{2}}^{2}}$=$\frac{{x}_{2}^{2}-{x}_{1}^{2}}{{x}_{1}^{2}{x}_{2}^{2}}$=$\frac{{(x}_{2}-{x}_{1}{)(x}_{2}+{x}_{1})}{{x}_{1}^{2}{x}_{2}^{2}}$,
∵x1<x2,且x1>0,x2>0
∴x2-x1>0,x2+x1>0,x12•x22>0,
∴$\frac{{(x}_{2}-{x}_{1}){(x}_{2}+{x}_{1})}{{x}_{1}^{2}{x}_{2}^{2}}$>0,即f(x1)-f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)=$\frac{1}{{x}^{2}}$(x>0)是减函数.
点评 本题考查的是反比例函数综合题,根据题中所给出的材料假设出x1<x2,且x1>0,x2>0,再比较出其大小即可.

 阅读快车系列答案
阅读快车系列答案| A. | 没有交点 | B. | 只有一个交点,且它位于y轴右侧 | ||
| C. | 有两个交点,且它们均位于y轴左侧 | D. | 有两个交点,且它们均位于y轴右侧 |
| A. | 93,96 | B. | 96,96 | C. | 96,100 | D. | 93,100 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 0 | D. | 2 |
 图中是对顶角量角器,用它测量角的原理是对顶角相等.
图中是对顶角量角器,用它测量角的原理是对顶角相等.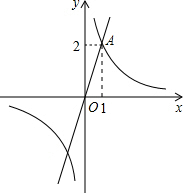 如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.
如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.