题目内容
7.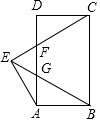 如图,在矩形ABCD中,BC=$\sqrt{3}$,AB=1,以BC为边作等边△BEC,CE,BE分别交AD于F,G两点,连接AE,则△AEF的周长等于$\sqrt{3}$+1.
如图,在矩形ABCD中,BC=$\sqrt{3}$,AB=1,以BC为边作等边△BEC,CE,BE分别交AD于F,G两点,连接AE,则△AEF的周长等于$\sqrt{3}$+1.
分析 由等边三角形性质得:EC=EB=BC=$\sqrt{3}$,∠ECB=60°,由矩形的四个角为直角得:∠DCF=90°-60°=30°,
根据30度角的正切得:tan30°=$\frac{DF}{DC}$=$\frac{\sqrt{3}}{3}$,求DF的长,由30°角所对的直角边是斜边的一半求FC的长,所以可以依次求EF和AF的长,证明△EFA≌△DFC,则AE=DC=1,计算△AEF的周长即可.
解答 解:∵△BEC是等边三角形,
∴EC=EB=BC=$\sqrt{3}$,∠ECB=60°,
∵四边形ABCD是矩形,
∴∠DCB=∠D=90°,
∴∠DCF=90°-60°=30°,
tan30°=$\frac{DF}{DC}$=$\frac{DF}{1}$=$\frac{\sqrt{3}}{3}$,
∴DF=$\frac{\sqrt{3}}{3}$,
∴FC=2DF=$\frac{2\sqrt{3}}{3}$,
∴EF=$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$,
AF=AD-DF=$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
∴DF=EF,AF=FC,
∵∠EFA=∠DFC,
∴△EFA≌△DFC,
∴AE=DC=1,
∴△AEF的周长=AE+EF+AF=1+$\frac{\sqrt{3}}{3}$+$\frac{2\sqrt{3}}{3}$=1+$\sqrt{3}$;
故答案为:$\sqrt{3}+1$.
点评 本题考查了矩形的性质、全等三角形的性质和判定、等边三角形的性质,以等边△BEC的性质为突破口,依次得出边和角的值,并利用全等三角形求出AE=CD是关键.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案| A. | a2+a2=2a4 | B. | 5y-3y=2 | C. | 3x2y-2yx2=x2y | D. | 3a+2b=5ab |
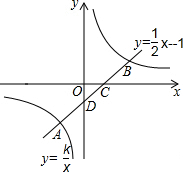 如图,已知直线y=$\frac{1}{2}$x-1与双曲线y=$\frac{k}{x}$相交于A,B两点,与x轴,y轴分别相交于C,D两点,已知AD=BC=2CD.
如图,已知直线y=$\frac{1}{2}$x-1与双曲线y=$\frac{k}{x}$相交于A,B两点,与x轴,y轴分别相交于C,D两点,已知AD=BC=2CD.