Question

6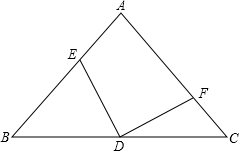．如图，在等腰直角△ABC中，∠A=90°，AB=AC，D为边BC中点，DE⊥DF，若BC=4，求四边形AEDF的面积．

Answer 1

分析 先连接AD，根据等腰直角三角形的性质，求得AD=CD=2，∠DAE=∠C=45°，∠ADE=∠CDF，进而判定△ADE≌△CDF，得出四边形AEDF的面积=△ACD的面积即可．

解答 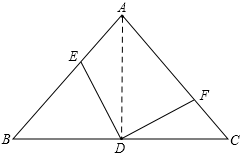解：连接AD，
∵∠A=90°，AB=AC，D为边BC中点，BC=4，
∴AD⊥BC，AD=CD=2，∠DAE=∠C=45°，
∴∠ADE+∠ADF=∠CDF+∠ADF=90°，
∴∠ADE=∠CDF，
在△ADE和△CDF中，
$\left\{\begin{array}{l}{∠DAE=∠C}\\{AD=CD}\\{∠ADE=∠CDF}\end{array}\right.$，
∴△ADE≌△CDF（ASA），
∴△ADE的面积=△CDF的面积，
∴四边形AEDF的面积=△ACD的面积=$\frac{1}{2}$×2×2=2．

点评 本题主要考查了等腰直角三角形的性质以及全等三角形的判定与性质，解决问题的关键是作辅助线构造全等三角形，将四边形AEDF的面积转化为△ACD的面积．