题目内容
依次连接等边△A1B1C1三边的中点,得到△A2B2C2,再依次连接△A2B2C2三边的中点得到△A3B3C3,按照此方法继续下去.已知等边△A1B1C1的边长为1,则△AnBnCn的面积为 .
考点:等边三角形的性质,三角形中位线定理
专题:规律型
分析:根据三角形中位线性质得到△A2B2C2,的边长为
,△A3B3C3的边长为(
)2,由此得到△AnBnCn的边长为(
)n-1,然后根据等边三角形的面积等于边长的
倍计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
解答:解:∵连接等边△A1B1C1三边的中点,得到△A2B2C2,等边△A1B1C1的边长为1,
∴△A2B2C2,的边长为
,
同样得△A3B3C3的边长为(
)2,
∴△AnBnCn的边长为(
)n-1,
∴△AnBnCn的面积=
[(
)n-1]2,
=
.
故答案为
.
∴△A2B2C2,的边长为
| 1 |
| 2 |
同样得△A3B3C3的边长为(
| 1 |
| 2 |
∴△AnBnCn的边长为(
| 1 |
| 2 |
∴△AnBnCn的面积=
| ||
| 4 |
| 1 |
| 2 |
=
| ||
| 4n |
故答案为
| ||
| 4n |
点评:本题考查了等边三角形的性质:等边三角形的三个内角都相等,且都等于60°;等边三角形的面积等于边长的
倍.也考查了三角形中位线性质.
| ||
| 4 |

练习册系列答案
相关题目
 已知a,b,c在数轴上的位置如图所示,化简|a+c|-|a-2b|-|c-2b|的结果是( )
已知a,b,c在数轴上的位置如图所示,化简|a+c|-|a-2b|-|c-2b|的结果是( )| A、0 | B、4b |
| C、-2a-2c | D、2a-4b |
下列四个数:-3、-
、0.3、0中比-2小的数是( )
| 3 |
| A、-3 | ||
B、-
| ||
| C、0 | ||
| D、0.3 |

 如图,在平面直角坐标系中,直线AC与x轴交于点A(4,0),与y轴交于点C(0,4).作OB⊥AC于点B,动点D在边OA上,D(m,0)(0<m<4),过点D作DE⊥OA交折线OB-BA于点E.Rt△GHI的斜边HI在射线AC上,GI∥OA,GI=m,GI与x轴的距离为
如图,在平面直角坐标系中,直线AC与x轴交于点A(4,0),与y轴交于点C(0,4).作OB⊥AC于点B,动点D在边OA上,D(m,0)(0<m<4),过点D作DE⊥OA交折线OB-BA于点E.Rt△GHI的斜边HI在射线AC上,GI∥OA,GI=m,GI与x轴的距离为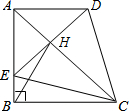 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论:
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论: 如图,抛物线y=ax2+bx+c顶点P坐标为(2,-1),与y轴交点坐标(0,3),将该抛物线沿图中P→Q方向平移
如图,抛物线y=ax2+bx+c顶点P坐标为(2,-1),与y轴交点坐标(0,3),将该抛物线沿图中P→Q方向平移