题目内容
2.在平面直角坐标系中,以原点为中心,把点A(4,5)逆时针旋转90°得到点B,则点B的坐标是(-5,4).分析 分别过A、B作x轴的垂线,垂足分别为C、D,可证明△AOC≌△OBD,可求得BD和OB的长,则可求得B点坐标.
解答  解:
解:
如图,分别过A、B作x轴的垂线,垂足分别为C、D,
∵A(4,5),
∴OC=4,AC=5,
∵把点A(4,5)逆时针旋转90°得到点B,
∴OA=OB,且∠AOB=90°,
∴∠BOD+∠AOC=∠AOC+∠CAO=90°,
∴∠BOD=∠CAO,
在△AOC和△OBD中
$\left\{\begin{array}{l}{∠ACO=∠BDO}\\{∠OAC=∠BOD}\\{OA=OB}\end{array}\right.$
∴△AOC≌△OBD(AAS),
∴OD=AC=5,BD=OC=4,
∴B(-5,4),
故答案为:(-5,4).
点评 本题主要考查旋转的性质,构造三角形全等求得线段的长度是解题的关键,注意旋转前后对应线段相等.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
17.下列说法正确的是( )
| A. | “姚明在罚球线上投篮一次,未投中”是不可能事件 | |
| B. | “任意画一个平行四边形,是中心对称图形”是随机事件 | |
| C. | “通常加热到100℃,水沸腾”是必然事件 | |
| D. | “购买一张彩票,中奖”是不可能事件 |
12.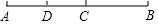 如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=10.5cm,那么BC的长为( )
如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=10.5cm,那么BC的长为( )
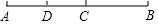 如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=10.5cm,那么BC的长为( )
如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=10.5cm,那么BC的长为( )| A. | A2.5cm | B. | 3cm | C. | 4.5cm | D. | 6cm |
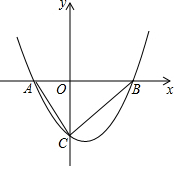 如图,已知二次函数y=x2-($\sqrt{3}$-m)x-$\sqrt{3}$m(其中0<m<$\sqrt{3}$)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,△ABC的外心为P.
如图,已知二次函数y=x2-($\sqrt{3}$-m)x-$\sqrt{3}$m(其中0<m<$\sqrt{3}$)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,△ABC的外心为P.
 如图,在矩形ABCD中,E为BC上一点,连接DE,过点A作AF⊥DE于点F,△DEC与△ADF相似吗?请说明理由.
如图,在矩形ABCD中,E为BC上一点,连接DE,过点A作AF⊥DE于点F,△DEC与△ADF相似吗?请说明理由.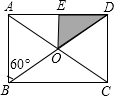 小明把如图所示的矩形纸板ABCD挂在墙上,E为AD中点,且∠ABD=60°,并用它玩飞镖游戏(每次飞镖均落在纸板上),击中阴影区域的概率是$\frac{1}{8}$.
小明把如图所示的矩形纸板ABCD挂在墙上,E为AD中点,且∠ABD=60°,并用它玩飞镖游戏(每次飞镖均落在纸板上),击中阴影区域的概率是$\frac{1}{8}$.