题目内容
6.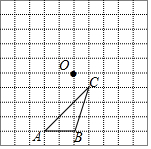 如图所示,△ABC与点O在10×10的网格中的位置如图所示,设每个小正方形的边长为1.
如图所示,△ABC与点O在10×10的网格中的位置如图所示,设每个小正方形的边长为1.(1)画出△ABC绕点O旋转180°后的图形;
(2)若⊙M能盖住△ABC,则⊙M的半径最小值为$\sqrt{5}$.
分析 (1)延长AO到点D使OD=OA,则点A的对应点为D,同样方法作出点B、C的对应点E、F,则△DEF与△ABC关于点O中心对称;
(2)作AB和AC的垂直平分线,它们的交点为△ABC的外心,而△ABC的外接圆为能盖住△ABC的最小圆,然后利用勾股定理计算出MA即可.
解答 解:(1)如图,△DEF为所作;
(2)如图,点M为△ABC的外心,MA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
故答案为$\sqrt{5}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
17.下列说法正确的是( )
| A. | “姚明在罚球线上投篮一次,未投中”是不可能事件 | |
| B. | “任意画一个平行四边形,是中心对称图形”是随机事件 | |
| C. | “通常加热到100℃,水沸腾”是必然事件 | |
| D. | “购买一张彩票,中奖”是不可能事件 |
18.下列方程的变形,符合等式的性质的是( )
| A. | 由2x-3=1,得2x=1-3 | B. | 由-2x=1,得x=-2 | ||
| C. | 由8-x=x-5,得-x-x=-5-8 | D. | 由2(x-3)=1,得2x-3=1 |
16.方程$\frac{x}{4}$=-$\frac{1}{2}$x+3的解为( )
| A. | x=4 | B. | x=$\frac{9}{4}$ | C. | x=-4 | D. | x=$\frac{3}{2}$ |
 一个几何体由大小相同的小立方块达成,从上面看到的几何体形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,已知物体的俯视图.请画出从正面和左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方块达成,从上面看到的几何体形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,已知物体的俯视图.请画出从正面和左面看到的这个几何体的形状图. 如图,在矩形ABCD中,E为BC上一点,连接DE,过点A作AF⊥DE于点F,△DEC与△ADF相似吗?请说明理由.
如图,在矩形ABCD中,E为BC上一点,连接DE,过点A作AF⊥DE于点F,△DEC与△ADF相似吗?请说明理由.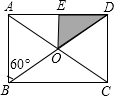 小明把如图所示的矩形纸板ABCD挂在墙上,E为AD中点,且∠ABD=60°,并用它玩飞镖游戏(每次飞镖均落在纸板上),击中阴影区域的概率是$\frac{1}{8}$.
小明把如图所示的矩形纸板ABCD挂在墙上,E为AD中点,且∠ABD=60°,并用它玩飞镖游戏(每次飞镖均落在纸板上),击中阴影区域的概率是$\frac{1}{8}$.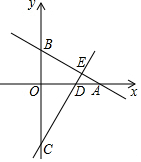 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+3与x轴、y轴交于点A、B.直线CD与y轴交于点C(0,-6),与x轴相交于点D,与直线AB相交于点E.若△AOB≌△COD,则点E的坐标为($\frac{18}{5}$,$\frac{6}{5}$).
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+3与x轴、y轴交于点A、B.直线CD与y轴交于点C(0,-6),与x轴相交于点D,与直线AB相交于点E.若△AOB≌△COD,则点E的坐标为($\frac{18}{5}$,$\frac{6}{5}$).