题目内容
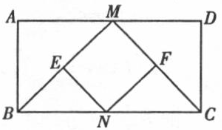
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中的点,E、F分别是线段BM、CM的中点.
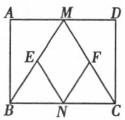
(1)求证:△ABM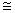 △DCM;
△DCM;
(2)当AB:AD为何值时,四边形MENF是正方形.
(1)证明: 四边形ABCD是矩形,
四边形ABCD是矩形,
 AB=DC,∠A=∠D=90°,…………………1分
AB=DC,∠A=∠D=90°,…………………1分
 M为AD的中点,
M为AD的中点, AM=DM,…………………………2分
AM=DM,…………………………2分
在△ABM和△DCM中
 AM=DM
AM=DM
∠A=∠D
AB=DC
 △ABM
△ABM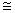 △DCM(SAS).…………………3分
△DCM(SAS).…………………3分
(2)当AB:AD=1:2时,四边形MENF是正方形,……………………4分
理由是: AB:AD=1:2,AM=DM,AB=CD,
AB:AD=1:2,AM=DM,AB=CD,
 AB-A=DM=DC,…………………………5分
AB-A=DM=DC,…………………………5分
 ∠A=∠D=90°,
∠A=∠D=90°,
 ∠ABM=∠AMB=∠DMC=∠DCM=45°,
∠ABM=∠AMB=∠DMC=∠DCM=45°,
 ∠BMC=90°………………6分
∠BMC=90°………………6分
 四边形ABCD是矩形,
四边形ABCD是矩形,
 ∠ABC=∠DCB=90°,
∠ABC=∠DCB=90°,
 ∠MBC= ∠MCB=45°,
∠MBC= ∠MCB=45°,
 BM=CM,………………………7分
BM=CM,………………………7分
 N、E、F分别是BC、BM、CM的中点,
N、E、F分别是BC、BM、CM的中点,
 BE=CF,ME=MF,NF∥BM,NE∥CM,
BE=CF,ME=MF,NF∥BM,NE∥CM,
 四边形AENF是平行四边形,…………………………8分
四边形AENF是平行四边形,…………………………8分
 AE=MF,∠BMC=90°,
AE=MF,∠BMC=90°,
 四边形MENF是正方形,
四边形MENF是正方形,
即当AB:AD=1:2时,四边形MENF是正方形。……………………9分

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目

 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有四个.其中正确的结论是_____________.(只填序号)
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有四个.其中正确的结论是_____________.(只填序号)
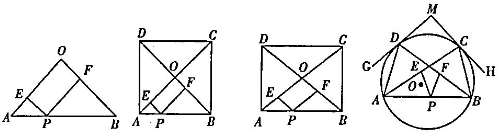 图1 图2 图3 图4
图1 图2 图3 图4