题目内容
3.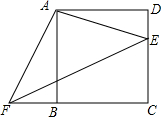 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.若BC=8,DE=3,求△AEF的面积.
四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.若BC=8,DE=3,求△AEF的面积.
分析 先利用勾股定理可计算出AE=$\sqrt{73}$,再根据△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90°得到AE=AF,∠EAF=90°,然后根据直角三角形的面积公式计算即可.
解答 解:四边形ABCD是正方形,BC=8,
∴AD=8,
在Rt△ADE中,DE=3,AD=8,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{73}$,
∵△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90度得到,
∴△ABF≌△ADE,
∴AE=AF,∠EAF=90°,
∴△AEF的面积=$\frac{1}{2}$AE2=$\frac{1}{2}$×73=$\frac{73}{2}$.
点评 本题考查了正方形的性质,全等三角形的判定与性质,旋转的性质以及勾股定理等知识点,解决本题的关键是明确△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90度得到,即△ABF≌△ADE.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
13.下列各式是完全平方式的是( )
| A. | x2-2x+1 | B. | 1+4x2 | C. | a2+ab+b2 | D. | x2+2x-1 |
14.今年某厂收益约有690万元,请将数690万用科学记数法表示为( )
| A. | 6.9×102 | B. | 6.9×103 | C. | 6.9×107 | D. | 6.9×106 |
15.关于函数$y=\frac{1}{3}x+2$,下列结论中,正确的是( )
| A. | 函数图象经过点(0,0) | B. | 函数图象不经过第四象限 | ||
| C. | y随x的增大而减小 | D. | 不论x为何值,总有y>0 |
 快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:
快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题: