题目内容
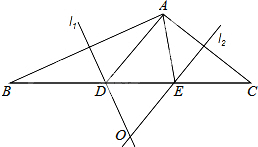 如图,在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,△ADE的周长为6cm.
如图,在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,△ADE的周长为6cm.(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长;
(3)若∠BAC=110°,则∠DAE=
考点:线段垂直平分线的性质
专题:
分析:(1)由在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,可得AD=BD,AE=CE,继而可得BC=△ADE的周长;
(2)由在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,可得OA=OB=OC,继而求得答案;
(3)由∠BAC=110°,可求得∠BVAD+∠CAE=∠ABC+∠ACB,继而求得答案.
(2)由在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,可得OA=OB=OC,继而求得答案;
(3)由∠BAC=110°,可求得∠BVAD+∠CAE=∠ABC+∠ACB,继而求得答案.
解答: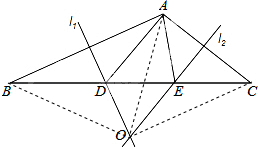 解:(1)∵在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,
解:(1)∵在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,
∴AD=BD,AE=CE,
∵△ADE的周长为6cm.
∴B=BD+DE+CE=AD+DE+AE=6cm;
(2)连结OA、OB、OC,
∵在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,
∴OA=OB,OA=OC,
∴OA=OB=OC,
∵△OBC的周长为16cm,
∴OB+OC+BC=16cm,
∴OB=OC=5cm,
∴OA=5cm;
(3)∵AD=BD,AE=CE,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∵∠BAC=110°,
∴∠ABC+∠ACB=70°,
∴∠BAD+∠EAC=70°,
∴∠DAE=∠BAC-(∠BAD+∠EAC)=40°.
故答案为:40.
 解:(1)∵在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,
解:(1)∵在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,∴AD=BD,AE=CE,
∵△ADE的周长为6cm.
∴B=BD+DE+CE=AD+DE+AE=6cm;
(2)连结OA、OB、OC,
∵在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,
∴OA=OB,OA=OC,
∴OA=OB=OC,
∵△OBC的周长为16cm,
∴OB+OC+BC=16cm,
∴OB=OC=5cm,
∴OA=5cm;
(3)∵AD=BD,AE=CE,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∵∠BAC=110°,
∴∠ABC+∠ACB=70°,
∴∠BAD+∠EAC=70°,
∴∠DAE=∠BAC-(∠BAD+∠EAC)=40°.
故答案为:40.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
在△ABC中,∠A=30°,∠B=60°,那么△ABC是( )
| A、等边三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、直角三角形 |