题目内容
解方程
(1)x2+10x+9=0(用配方法)
(2)(x-4)2=(5-2x)2.
(1)x2+10x+9=0(用配方法)
(2)(x-4)2=(5-2x)2.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)把常数项移到右边,两边加上一次项系数一半的平方,左边配成完全平方的形式,再用直接开平方求出方程的根.
(2)先移项得到(2x-3)2-(x-5)2=0,然后利用因式分解法解方程.
(2)先移项得到(2x-3)2-(x-5)2=0,然后利用因式分解法解方程.
解答:解:(1)x2+10x=-9,
x2+10x+25=16,
(x+5)2=16,
x+5=±4,
x=-5±4,
∴x1=-1,x2=-9.
(2)(x-4)2=(5-2x)2,
(x-4)2-(5-2x)2=0,
(x-4+5-2x)(x-4-5+2x)=0,
(-x+1)(3x-9)=0,
-x+1=0,或3x-9=0,
则x1=1,x2=3.
x2+10x+25=16,
(x+5)2=16,
x+5=±4,
x=-5±4,
∴x1=-1,x2=-9.
(2)(x-4)2=(5-2x)2,
(x-4)2-(5-2x)2=0,
(x-4+5-2x)(x-4-5+2x)=0,
(-x+1)(3x-9)=0,
-x+1=0,或3x-9=0,
则x1=1,x2=3.
点评:本题考查了解一元二次方程-因式分解法、配方法,用配方法解一元二次方程,把常数项移到右边,两边加上一次项系数一半的平方,左边配成完全平方的形式,再用直接开平方求出方程的根.因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
相关题目
在-3,-1
,0,-
,2002各数中,是正数的有( )
| 1 |
| 2 |
| 3 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
下列说法中错误的是( )
A、
| ||
B、
| ||
| C、-27的立方根是-3 | ||
| D、1是(-1)2的算术平方根 |
 如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.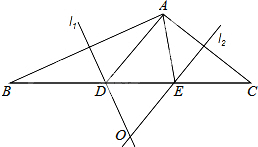 如图,在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,△ADE的周长为6cm.
如图,在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,△ADE的周长为6cm.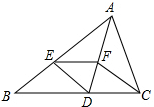 如图,△ABC中,AD平分∠BAC交BC于点D,在线段AB上截取AE=AC,过点E作EF∥BC交AD于点F.
如图,△ABC中,AD平分∠BAC交BC于点D,在线段AB上截取AE=AC,过点E作EF∥BC交AD于点F.