题目内容
16.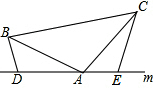 如图,在△ABC中,AB=AC,D,A,E三点都在一条直线上,且∠BDA=∠AEC=∠BAC,BD=3,CE=6,则DE的长为9.
如图,在△ABC中,AB=AC,D,A,E三点都在一条直线上,且∠BDA=∠AEC=∠BAC,BD=3,CE=6,则DE的长为9.
分析 由条件可知∠BDA=∠AEC=∠BAC,可得∠DBA=∠CAE,结合条件可证明△ABD≌△CAE,利用全等三角形的性质解答即可.
解答 解:∵∠BDA=∠AEC=∠BAC,
∴∠DBA+∠BAD=∠BAD+∠CAE,
∴∠DBA=∠CAE,
∵在△ADB和△CEA中,
$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠AEC}\\{AB=CA}\end{array}\right.$,
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE=3+6=9.
故答案为:9.
点评 本题主要考查全等三角形的判定和性质,由条件证明三角形全等得到BD=AE、CE=AD是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
6.在同一直角坐标系中,直线y1=x+b与直线y2=ax-1交于点(-2,1),
(1)求a,b的值,并在同一直角坐标系中画出两个函数的图象;
(2)利用图象求出:当x取何值时有①y1>y2,②y1<0.
(1)求a,b的值,并在同一直角坐标系中画出两个函数的图象;
(2)利用图象求出:当x取何值时有①y1>y2,②y1<0.
1.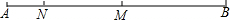 如图,已知点M是线段AB上的中点,N是线段AM上的点,且满足AN:MN=1:2,若AN=1.5cm,则线段AB=( )
如图,已知点M是线段AB上的中点,N是线段AM上的点,且满足AN:MN=1:2,若AN=1.5cm,则线段AB=( )
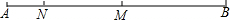 如图,已知点M是线段AB上的中点,N是线段AM上的点,且满足AN:MN=1:2,若AN=1.5cm,则线段AB=( )
如图,已知点M是线段AB上的中点,N是线段AM上的点,且满足AN:MN=1:2,若AN=1.5cm,则线段AB=( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 9cm |
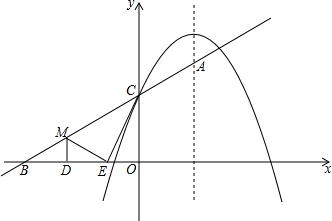
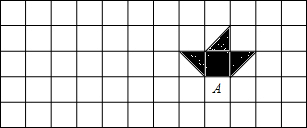 如图所示,图中的小船A是由一艘小船B先向右平移三格,再向上平移2格后得到的,请你画出原来的小船B,并求出此时小船的面积.(图中每一小格的边长为1)
如图所示,图中的小船A是由一艘小船B先向右平移三格,再向上平移2格后得到的,请你画出原来的小船B,并求出此时小船的面积.(图中每一小格的边长为1)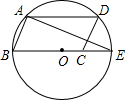 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=70°,连接
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=70°,连接