题目内容
 已知如图,直线AB∥CD,直线EF与直线AB交于M,与直线CD交于N,且MP平分∠EMB.试说明:∠4=
已知如图,直线AB∥CD,直线EF与直线AB交于M,与直线CD交于N,且MP平分∠EMB.试说明:∠4=| 1 |
| 2 |
考点:平行线的性质
专题:证明题
分析:由直线AB∥CD,可得:∠EMB=∠2,由MP平分∠EMB,可得∠4=
∠EMB,进而得到∠4=
∠2,然后根据对顶角相等可得∠1=∠2,进而可得:∠4=
∠1.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵AB∥CD,
∴∠EMB=∠2,
∴MP平分∠EMB,
∴∠4=
∠EMB,
∴∠4=
∠2,
∵∠1=∠2,
∴∠4=
∠1.
∴∠EMB=∠2,
∴MP平分∠EMB,
∴∠4=
| 1 |
| 2 |
∴∠4=
| 1 |
| 2 |
∵∠1=∠2,
∴∠4=
| 1 |
| 2 |
点评:此题考查了平行线的性质:两直线平行,同位角相等;同位角相等,两直线平行.也考查了角平分线的定义.

练习册系列答案
相关题目
某果园2012年水果产量为100吨,2014年水果产量为144吨,则该果园水果产量的年平均增长率为多少?若设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
| A、144(1-x)2=100 |
| B、100(1-x)2=144 |
| C、144(1+x)2=100 |
| D、100(1+x)2=144 |
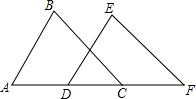 如图,已知AB∥DE,BC∥EF,C在AF上,且AD=CF,△ABC与△DEF全等吗?请说明理由.
如图,已知AB∥DE,BC∥EF,C在AF上,且AD=CF,△ABC与△DEF全等吗?请说明理由.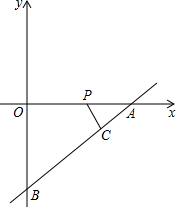 如图,直线y=
如图,直线y= 如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.
如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.