题目内容
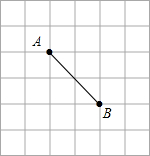在如图的网格中，在网格上找到点C，使△ABC为等腰三角形，这样的点有几个（ ）| A、8 | B、9 | C、10 | D、11 |
考点：等腰三角形的判定
专题：网格型
分析：首先由勾股定理可求得AB的长，然后分别从BA=BC，AB=AC，CA=CB去分析求解即可求得答案．
解答：解：如图，
∵AB=
=2
，
∴①若BA=BC，则符合要求的有：C1，C2共2个点；
②若AB=AC，则符合要求的有：C3，C4共2个点；
③若CA=CB，则符合要求的有：C5，C6，C7，C8，C9，C10共6个点．
∴这样的C点有10个．
故选：C．
∵AB=
| 22+22 |
| 2 |
∴①若BA=BC，则符合要求的有：C1，C2共2个点；
②若AB=AC，则符合要求的有：C3，C4共2个点；
③若CA=CB，则符合要求的有：C5，C6，C7，C8，C9，C10共6个点．
∴这样的C点有10个．
故选：C．
点评：本题考查了等腰三角形的判定以及勾股定理，解题关键是分类的数学思想．
练习册系列答案
阅读快车系列答案
相关题目
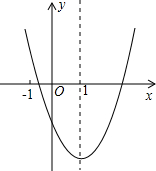已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论错误的是（ ）| A、abc＞0 |
| B、2a+b=0 |
| C、a-b+c＞0 |
| D、4a+2b+c＞0 |
一扇形的半径为12cm，若此扇形围成的圆锥的底面半径为10cm，那么这个扇形的面积是（ ）
| A、60πcm2 |
| B、120πcm2 |
| C、240πcm2 |
| D、480πcm2 |
如图，在梯形ABCD中，AD∥BC，将腰AB沿底BC平移至DM，若点M恰好是BC的中点，那么点N是DM的中点吗？写出你的结论并说明理由．数m和n，满足m为正数，n为负数，则m，m-n，m+n的大小关系是（ ）
| A、m＞m-n＞m+n |
| B、m+n＞m＞m-n |
| C、m-n＞m+n＞m |
| D、m-n＞m＞m+n |
抛物线二次函数y=x2的图象向左平移2个单位，得到新的图象的二次函数表达式是（ ）
| A、y=x2+2 |
| B、y=（x+2）2 |
| C、y=（x-2）2 |
| D、y=x2-2 |