题目内容
 如图,在梯形ABCD中,AD∥BC,将腰AB沿底BC平移至DM,若点M恰好是BC的中点,那么点N是DM的中点吗?写出你的结论并说明理由.
如图,在梯形ABCD中,AD∥BC,将腰AB沿底BC平移至DM,若点M恰好是BC的中点,那么点N是DM的中点吗?写出你的结论并说明理由.考点:平移的性质
专题:
分析:根据平移的性质可得AB∥DM,AB=DM,然后判断出四边形ABMD是平行四边形,再根据平行四边形的对边相等可得AD=BM,再求出AD=CM,然后根据一组对边平行且相等的四边形是平行四边形判断出四边形AMCD是平行四边形,然后根据平行四边形的对角线互相平分解答即可.
解答:解:∵AB沿底BC平移至DM,
∴AB∥DM,AB=DM,
∴四边形ABMD是平行四边形,
∴AD=BM,
∵点M恰好是BC的中点,
∴BM=CM=AD,
∵AD∥BC,
∴四边形AMCD是平行四边形,
∴点N是DM的中点.
∴AB∥DM,AB=DM,
∴四边形ABMD是平行四边形,
∴AD=BM,
∵点M恰好是BC的中点,
∴BM=CM=AD,
∵AD∥BC,
∴四边形AMCD是平行四边形,
∴点N是DM的中点.
点评:本题考查了平移的性质,平行四边形的判定与性质,熟记各性质并求出四边形AMCD是平行四边形是解题的关键.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
在
,1.4,-π,3.
,-9中,无理数有( )
| 2 |
| • |
| 2 |
| • |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
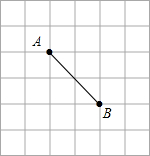 在如图的网格中,在网格上找到点C,使△ABC为等腰三角形,这样的点有几个( )
在如图的网格中,在网格上找到点C,使△ABC为等腰三角形,这样的点有几个( )| A、8 | B、9 | C、10 | D、11 |
将△ABC向左平移2个单位长度后得到△A′B′C′.若点A的坐标是(-3,7),则点A′的坐标是( )
| A、(-5,5) |
| B、(-1,9) |
| C、(-5,7) |
| D、(-1,7) |
将抛物线y=x2向左平移6个单位,再向下平移8个单位后的抛物线为( )
| A、y=(x+6)2-8 |
| B、y=(x-6)2+8 |
| C、y=(x-6)2-8 |
| D、y=(x+6)2+8 |