题目内容

11．用11到2014这些自然数依次组成下列算式：1112+1314，1516+1718，1920+2122，2324+2526，…，20112012+20132014．其中，值能被4整除的算式有（　　）
A．0个B．125个C．250个D．499个

分析 根据题目中的式子发现各个式子之间的关系，根据结果可以判断题目中的式子是否能被4整除，本题得以解决．

解答 解：∵用11到2014这些自然数依次组成下列算式：1112+1314，1516+1718，1920+2122，2324+2526，…，20112012+20132014，
∴1112+1314=2426不能被4整除，
1516+1718=2426+808不能被4整除，
1920+2122=2426+808×2不能被4整除，
2324+2526=2426+808×3不能被4整除，
…
20112012+20132014不能被4整除，
故选A．

点评 本题考查式子的变化规律，解题的关键是找出各个式子间的规律．

练习册系列答案
相关题目
1．把多项式4x3y3-xy+2x4-8按字母x的降幂排列：2x4+4x3y3-xy-8．
2．下列各点中，在双曲线y=$\frac{3}{x}$上的点是（　　）
A．（ $\frac{1}{3}$，-9）B．（3，1）C．（-1，3）D．（6，-$\frac{1}{2}$ ）
19．计算：2015×（$\frac{1}{2}$-1）×（$\frac{1}{3}$-1）×（$\frac{1}{4}$-1）×…×（$\frac{1}{2015}$-1）=1．
6．如图，已知二次函数图象的顶点坐标为（2，0），直线y=x+1与二次函数的图象交于A，B两点，其中点A在y轴上．
（1）求二次函数的解析式；
（2）证明：点（-m，2m-1）不在（1）中所求的二次函数的图象上；
（3）若E点的横坐标为4，过E作x轴的垂线交直线y=x+1于点C，交二次函数的图象于D点，二次函数的图象上是否存在点P，使得S△POE=2S△ABD？若存在，求出P点坐标，若不存在，请说明理由．
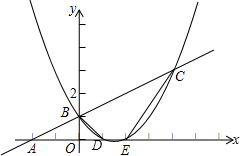2．如图，已知一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A，与y轴交于点B，二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于点B、C两点，与x轴交于D、E两点，且D点坐标为（1，0）．
（1）求二次函数的解析式；
（2）在在x轴上有一动点P，从O点出发以每秒1个单位的速度沿x轴向右运动，是否存在动点P，使得△PBC是以P为直角顶点的直角三角形？若存在，求出点P运动时间t的值；若不存在，请说明理由；
（3）若动点P在x轴上，动点Q在射线AC上，同时从A点出发，点P沿x轴正方向以每秒2个单位的速度运动，点Q以每秒a个单位的速度沿射线AC运动，是否存在以A、P、Q为顶点的三角形与△ABD相似？若存在，求a的值；若不存在，说明理由．
9．在四边形ABCD中，M是AB边上的动点，点F在AD的延长线上，且DF=DC，N为MD的中点．连接BN，CN，作NE⊥BN交直线CF于点E．
（1）如图1，若四边形ABCD为正方形，当点M与A重合时，求证；NB=NC=NE；
（2）如图2，若四边形ABCD为正方形，当点M与A不重合时，（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；
（3）如图3，若四边形ABCD为矩形，当点M与A不重合，点E在FC的延长线上时，请你就线段NB，NC，NE提出一个正确的结论．（不必说理）
6．若|x|=5，|y|=9，则x+y=4或-14或14或-4，x-y=-14或4或-4或14．
7．重庆市巴川中学是全国啦啦操基地，每届学生对啦啦操技巧的掌握都将得到传承，初2008级的同学们本周正在认真学习啦啦操，为庆“六一”表演积极做准备．学校艺体处为了解同学们跳啦啦操的热情和喜爱情况，组织大队委对本年级学生进行随机抽样调查．大队委文艺副部长小王对抽样的同学们对啦啦操的喜爱程度分为四类：A：非常喜欢；B：比较喜欢；C：一般喜欢；D：不喜欢，并将自己的调查结果绘制成如图的统计图，请你结合图中所给信息解答下列问题：

请将条形统计图补充完整；初2008级共有学生2400人，请你用小王的调查结果估计该年级“非常喜欢”和“比较喜欢”跳啦啦操的人数之和有多少人？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网