题目内容
20.在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )| A. | (2,0) | B. | (4,0) | C. | (-2,0) | D. | (0,0) |
分析 作A关于x轴的对称点C,连接BC交x轴于P,连接AP,此时点P到点A和点B的距离之和最小,先求出C的坐标,设直线CB的解析式是y=kx+b,把C、B的坐标代入求出解析式是y=x-2,把y=0代入求出x即可.
解答 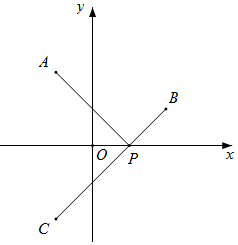 解:作A关于x轴的对称点C,连接BC交x轴于P,连接AP,则此时AP+PB最小,
解:作A关于x轴的对称点C,连接BC交x轴于P,连接AP,则此时AP+PB最小,
即此时点P到点A和点B的距离之和最小,
∵A(-2,4),
∴C(-2,-4),
设直线CB的解析式是y=kx+b,
把C、B的坐标代入得:
$\left\{\begin{array}{l}{2=4k+b\\;}\\{-4=-2k+b}\end{array}\right.$,
解得:k=1,b=-2,
∴y=x-2,
把y=0代入得:0=x-2,
解得x=2,
即P的坐标是(2,0),
故选A.
点评 本题考查了轴对称-最短路线问题,一次函数的解析式,坐标与图形性质等知识点的运用,解题的关键是根据轴对称的性质画出P的位置.凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (b-a)2=b2-2ab+a2 | C. | (a+2b)(a-2b)=a2-2b2 | D. | (a-b)2=a2-2ab-b2 |
11.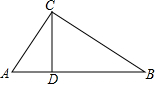 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )
 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )| A. | BD=a•sinα | B. | AD=$\frac{a•sinα}{tanα}$ | C. | AC=$\frac{a}{sinα}$ | D. | CD=a•cosα |
8.下列因式分解正确的是( )
| A. | a2b-2a3=a(ab-2a2) | B. | x2-x+$\frac{1}{4}$=${(x-\frac{1}{2})}^{2}$ | C. | x2+2x+1=x(x+2)+1 | D. | 4x2-y2=(4x+y)(4x-y) |
12.下列运算中,正确的是( )
| A. | 3a+2b=5ab | B. | 2a3+3a2=5a5 | C. | 4a2b-3ba2=a2b | D. | 5a2-4a2=1 |
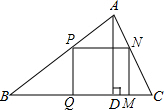 如图,△ABC是一块锐角三角形余料,边BC=12厘米,高AD=8厘米,要把它加工成矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上
如图,△ABC是一块锐角三角形余料,边BC=12厘米,高AD=8厘米,要把它加工成矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上 如图,数轴上点A、B、C所对应的数分别为a、b、c,化简|a|+|c-b|-|a+b-c|=0.
如图,数轴上点A、B、C所对应的数分别为a、b、c,化简|a|+|c-b|-|a+b-c|=0.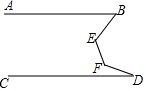 如图,AB∥CD,∠B=42°,∠D=17°,求∠E+∠F的度数.
如图,AB∥CD,∠B=42°,∠D=17°,求∠E+∠F的度数.