题目内容
15.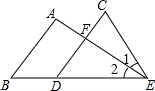 已知,如图,AB∥CD,∠A=95°,∠C=65°,∠1:∠2=3:4,求∠B的度数.
已知,如图,AB∥CD,∠A=95°,∠C=65°,∠1:∠2=3:4,求∠B的度数.
分析 先根据平行线的性质求得∠BFD的度数,再根据外角性质,求得∠1及∠2的度数,最后根据三角形内角和定理,求得∠B的度数.
解答  解:∵AB∥CD,
解:∵AB∥CD,
∴∠A=∠DFE=95°,
∵∠C=65°,
∴∠1=95°-65°=30°,
∵∠1:∠2=3:4,
∴∠2=40°,
∴△ABE中,∠B=180°-95°-40°=45°.
点评 本题主要考查了平行线的性质,解决问题的关键是运用三角形外角性质与内角和定理计算角度.两条平行线被第三条直线所截,同位角相等. 即两直线平行,同位角相等.

练习册系列答案
相关题目
10.已知a>b,若c是任意实数,则下列不等式中总成立的是( )
| A. | a+c<b+c | B. | a-c>b-c | C. | ac<bc | D. | ac>bc |
7.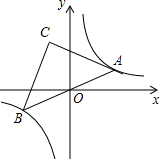 如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
 如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )| A. | y=$\frac{8}{x}$ | B. | y=$\frac{16}{x}$ | C. | y=-$\frac{16}{x}$ | D. | y=-$\frac{8}{x}$ |
4.已知直线y=kx+b与y=2x-5平行且经过点(1,3),则y=kx+b的表达式是( )
| A. | y=x+2 | B. | y=2x+1 | C. | y=2x+2 | D. | y=2x+3 |
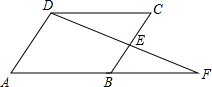 如图,在菱形ABCD中,点E是BC的中点,连接DE并延长与AB的延长线交于点F.
如图,在菱形ABCD中,点E是BC的中点,连接DE并延长与AB的延长线交于点F.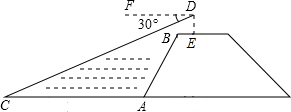 如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:$\sqrt{3}$≈1.73)
如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:$\sqrt{3}$≈1.73) 在下面网格图中,每个小正方形的边长为1,平移△ABC,使点A平移到点D.
在下面网格图中,每个小正方形的边长为1,平移△ABC,使点A平移到点D.