题目内容
11.解方程(组)(1)15-(7-5x)=2x+(5-3x)
(2)$\frac{3+0.2x}{0.2}$-$\frac{0.2+0.03x}{0.01}$=0.75
(3)$\left\{\begin{array}{l}{2x-7y=8}\\{3x-8y-10=0}\end{array}\right.$
(4)$\left\{\begin{array}{l}{3x-2y+4=0}\\{3y+2x-19=0}\end{array}\right.$
(5)$\left\{\begin{array}{l}{\frac{x+3}{2}+\frac{y+5}{3}=7}\\{\frac{x-4}{3}+\frac{2y-3}{5}=2}\end{array}\right.$
(6)$\left\{\begin{array}{l}{x+y=1}\\{y+z=2}\\{z+x=3}\end{array}\right.$.
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解.
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)此题先将3x-8y-10=0变为:3x-8y=10,此题可运用加减消元法消去y,将①×3-②×2可得出y的值,再将y代入任意一式即可得出y的值.
(4)方程组整理后,利用加减消元法求出解即可.
(5)方程组利用加减消元法求出解即可.
解答 解:(1)去括号得:15-7+5x=2x+5-3x,
移项合并得:6x=-3,
解得:x=-$\frac{1}{2}$;
(2)去分母得:2(30+2x)-4(20+3x)=3,
去括号得:60+4x-80-12x=3
移项合并得:-8x=23,
解得:x=-$\frac{23}{8}$;
(3)解:原方程组变为:$\left\{\begin{array}{l}{2x-7y=8①}\\{3x-8y=10②}\end{array}\right.$,
①×3-②×2得:
-5y=4,
y=-$\frac{4}{5}$,
再代入①得:
x=$\frac{6}{5}$,
∴原方程的解为$\left\{\begin{array}{l}{x=\frac{6}{5}}\\{y=-\frac{4}{5}}\end{array}\right.$;
(4)方程组整理得:$\left\{\begin{array}{l}{3x-2y=-4①}\\{2x+3y=19②}\end{array}\right.$,
①×3+②×2得:13x=26,即x=2,
把x=2代入①得:y=5,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$;
(5)方程组整理得:$\left\{\begin{array}{l}{3x+2y=23①}\\{5x+6y=59②}\end{array}\right.$,
①×3-②得:4x=10,
解得:x=$\frac{5}{2}$
把x=$\frac{5}{2}$代入①得:$\frac{15}{2}$+2y=23,
解得:y=$\frac{31}{4}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{31}{4}}\end{array}\right.$;
(6)$\left\{\begin{array}{l}{x+y=1①}\\{y+z=2②}\\{z+x=3③}\end{array}\right.$,
③-②得:x-y=1④,
④+①得:2x=2,即x=1,
把x=1代入①得:y=0,
把y=0代入②得:z=2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组和三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

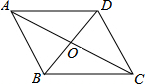 如图,AB∥CD,AD∥BC,AC与BD交于点O,那么图中全等的三角形共有4对.
如图,AB∥CD,AD∥BC,AC与BD交于点O,那么图中全等的三角形共有4对.