题目内容
 如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,D是△ABC外一点,且△ADC≌△APB,求∠APC的度数.
如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,D是△ABC外一点,且△ADC≌△APB,求∠APC的度数.考点:等边三角形的性质,全等三角形的性质
专题:
分析:利用△ABC为等边三角形,得出∠BAC=60°;连接DP,利用△ADC≌△APB,得出∠DAC=∠PAB,DA=PA,进一步得出△DAP是正三角形;利用勾股定理的逆定理得出△DCP为直角三角形,问题得解.
解答:解:如图,
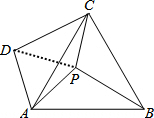
连接DP,
∵△ABC是正三角形,
∴∠BAC=60°,
∵△ADC≌△APB,
∴∠DAC=∠PAB,DA=PA,DC=PB,
∵∠PAC+∠BAP=60°,
∴∠PAC+∠CAD=60°,
∴△DAP是正三角形,
∴DP=6,∠DPA=60°;
在△PDC中.
PC=8,DP=6,DC=10,
∵82+62=102,
∴∠DPC=90°,
∴∠APC=∠DPA+∠DPC=60°+90°=150°.

连接DP,
∵△ABC是正三角形,
∴∠BAC=60°,
∵△ADC≌△APB,
∴∠DAC=∠PAB,DA=PA,DC=PB,
∵∠PAC+∠BAP=60°,
∴∠PAC+∠CAD=60°,
∴△DAP是正三角形,
∴DP=6,∠DPA=60°;
在△PDC中.
PC=8,DP=6,DC=10,
∵82+62=102,
∴∠DPC=90°,
∴∠APC=∠DPA+∠DPC=60°+90°=150°.
点评:此题考查等边三角形的判定与性质、三角形全等的性质、勾股定理的逆定理等知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个正方形的边长减少了3厘米,它的面积减少了39平方厘米,那么这个正方形的边长为( )
| A、5厘米 | B、6厘米 |
| C、8厘米 | D、10厘米 |
在平面直角坐标系中,如果直线y=k1x与双曲线y=
有交点,那么k1和k2的关系是( )
| k2 |
| x |
| A、k1<0,k2>0 |
| B、k1>0,k2<0 |
| C、k1、k2同号 |
| D、k1、k2异号 |
