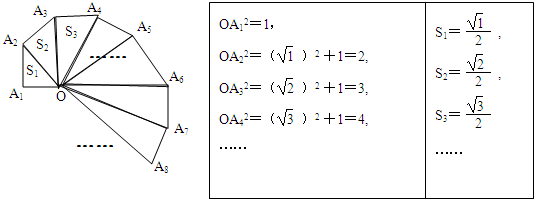题目内容
8．
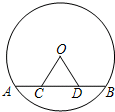如图，AB是⊙O的弦，点C、D在AB上，且AC=BD．判断△OCD的形状，并说明理由．
分析 根据全等三角形的判定，可得OC与OD的关系，根据等腰三角形的判定，可得答案．
解答 解：△OCD为等腰三角形，理由如下：
连接OA、OB
，
∵在⊙O中，OA=OB，
∴∠A=∠B．
∴在△OCA和△ODB中，
$\left\{\begin{array}{l}{OA=OB}\\{∠A=∠B}\\{AC=BD}\end{array}\right.$
∴△OCA≌△ODB（SAS），
∴OC=OD，
∴△OCD为等腰三角形．
点评 本题考查了全等三角形的判定与性质，等腰三角形的判定，利用全等三角形的判定与性质得出OC=OD是解题关键．
练习册系列答案
相关题目
如图，在△ABC中，AB=AC，点D在AC上，且BD=AD，∠A=36°，则∠DBC=36°．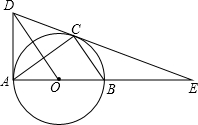
如图，AB是⊙O的直径，点C在⊙O上，连接BC、AC，作OD∥BC，与过点A的切线交于点D，连接DC并延长交AB的延长线于点E
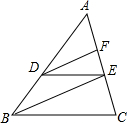如图，在△ABC中，D是AB 上一点，且$\frac{AD}{DB}$=$\frac{3}{2}$，E、F是AC上的点，且DE∥BC，DF∥BE，AF=9．求EC的长．
如图，点P在⊙O外，PB交⊙O于A、B两点，PC交⊙O于D、C两点．
20．正方形ABCD中，E，F分别为AB，BC的中点，AF与DE相交于点O，则$\frac{DO}{AD}$=（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{5}$$\sqrt{5}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |
