题目内容
有7000多根牙签,按以下6种规格分成小包:如果10根一包,最后还剩9根;如果9根一包,最后还剩8根;如果依次以8、7、6、5根为一包,最后分别剩7、6、5、4根.原来一共有牙签多少根?
考点:约数与倍数
专题:
分析:根据10根一包,最后还剩9根;如果9根一包,最后还剩8根;如果依次以8、7、6、5根为一包,最后分别剩7、6、5、4根.可以推知此数加上1就是10、9、8、7、6、5的公倍数,故求出10、9、8、7、6、5的公倍数减去1即可求解.
解答:解:这个数+1=10、9、8、7、6、5的公倍数,
10、9、8、7、6、5的公倍数为:5×2×3×3×4×7=2520,
满足(7000多)的10、9、8、7、6、5的公倍数2520×3=7560,牙签的数量是7560-1=7559(根).
答:原来一共有牙签7559根.
10、9、8、7、6、5的公倍数为:5×2×3×3×4×7=2520,
满足(7000多)的10、9、8、7、6、5的公倍数2520×3=7560,牙签的数量是7560-1=7559(根).
答:原来一共有牙签7559根.
点评:考查了约数与倍数,解题的关键是找到符合条件(7000多)的10、9、8、7、6、5的公倍数,再用它减去1即可.

练习册系列答案
相关题目
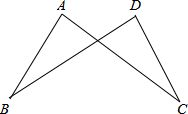 已知AB=DC,BD=CA,那么∠A与∠D相等吗,说明理由.
已知AB=DC,BD=CA,那么∠A与∠D相等吗,说明理由.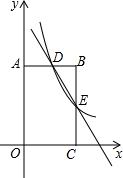 如图,四边形OABC为矩形,以点O为原点建立直角坐标系,点C在x轴的正半轴上,点A在y轴的正半轴上,已知点B为(2,4),反比例函数y=
如图,四边形OABC为矩形,以点O为原点建立直角坐标系,点C在x轴的正半轴上,点A在y轴的正半轴上,已知点B为(2,4),反比例函数y=